Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bản chất của bài này la tim GTNN của y = |x-2| + 1
y min <=> |x-2| min <=> x=2
Vậy điểm thấp nhất của đồ thị lả tại x=2 và y=1
Tick nha


chỉ cần cho 2 vế = nhau là được vì cắt nhau trên trục hoành thì y=0

Vì đồ thị hàm số đi qua điểm (5;-3) nên x=5, y=-3
Thay x=5, y=-3 vào CTHS y=(3m-1)x+4n-2 ta có
\(\Rightarrow\) -3=(3m-1)5 +4n -2
\(\Rightarrow\) -3=15m-5+4n-2
\(\Rightarrow\) 15m+3n=-4
\(\Rightarrow\) m=\(\frac{-4-3n}{15}\)(1)
Vì đồ thị hàm số cắt trục hoành tại điểm có tung độ là -2 nên x=-2 , y=0
Thay x=-2, y=0 vào CTHS y=(3m-1)x+4n-2 ta có
0=(3m-1)-2+4n-2
\(\Rightarrow\)0=-6m+2+4n-2
\(\Rightarrow\)-6m+4n=0
\(\Rightarrow\)m=\(\frac{4n}{-6}\)(2)
Từ 1 và 2 ta có
\(\frac{-4-3n}{15}\)=\(\frac{4n}{-6}\)
\(\Leftrightarrow\)24+18n=60n
\(\Leftrightarrow\)24=42n
\(\Leftrightarrow\)n=1,75
Thay n=1,75 vào (1) ta có
m=\(\frac{-4-3\cdot1,75}{15}\)
\(\Leftrightarrow\)m=\(\frac{-37}{60}\)
Vậy n=1,75 ;m=\(\frac{-37}{60}\)thì thoả mãn yêu cầu của đề bài
CHÚC BẠN HỌC TỐT

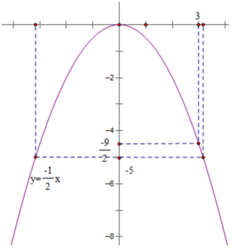
a) Từ đồ thị, ta xác định được tung độ của điểm D là (-9)/2
Với x = 3 ta có: y = ( - 1 ) / 2 x 2 = ( - 1 ) / 2 . 3 2 = ( - 9 ) / 2
Hai kết quả là như nhau.
b) Có 2 điểm có tung độ bằng -5
Giá trị của hoành độ của hai điểm lần lượt là ≈ -3,2 và ≈ 3,2

a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2)
(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2
<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3
Vậy (d) : y = -2x - 2
b, bạn tự vẽ nhé
c, Cho x = 0 => y = -2
=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2
Cho y = 0 => x = -1
=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1
Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt )
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1 <=> \hept{m=−3m≠92\hept{m=−3m≠92 <=> m=−3
Giả sử (d) luôn đi qua điểm cố định M(x0; y0)
Ta có: y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10
<=> mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0
<=> m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0
Để M cố định thì: \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0 <=> \hept{x0=−2y0=−20\hept{x0=−2y0=−20
Vậy...