Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

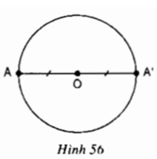
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)

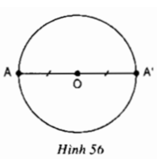
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)

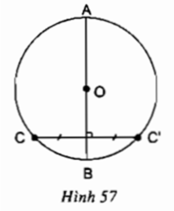
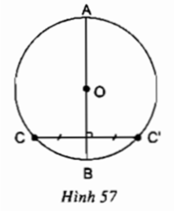
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)

Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)

a. AB là tiếp tuyến của đt (O) tại B (gt) => \(\widehat{OBA}=90^o\)
AC là tiếp tuyến của đt (O) tại C (gt) => \(\widehat{OCA}=90^o\)
Xét tứ giác ABOC có: \(\widehat{OBA}+\widehat{OCA}=90^o+90^o=180^o\)=> Tứ giác ABOC nội tiếp đường tròn (Dhnb) => Đpcm
b.
Xét đt (O) có: \(\widehat{ABD}=\frac{1}{2}sđ\widebat{BD}\)(T/c góc tạo bởi tiếp tuyến và dây cung)
\(\widehat{BED}=\widehat{BEA}=\frac{1}{2}sđ\widebat{BD}\)(T/c góc nội tiếp của đt) (Do A,D,E (gt) => \(\widehat{BED}=\widehat{BEA}\))
=> \(\widehat{ABD}=\widehat{BEA}\)
Xét \(\Delta ABD\)và \(\Delta AEB\)có:
* \(\widehat{A}chung\)
* \(\widehat{ABD}=\widehat{BEA}\left(cmt\right)\)
=> \(\Delta ABD~\Delta AEB\left(g.g\right)\)=> \(\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AB^2=AD.AE\RightarrowĐpcm\)
c. Vì F là điểm đối xứng của D qua OA => OA là đường trung trực của DF (Đ/n đối xứng trục) => OD = OF = R (T/c điểm thuộc đường trung trực) => F \(\in\left(O\right)\)và \(\Delta ODF\)cân tại O (Đ/n) => OA vừa là đường trung trực của đoạn thẳng DF đồng thời là đường phân giác của \(\widehat{DOF}\)(T/c của \(\Delta\)cân)=> \(\widehat{DOA}=\widehat{FOA}=\frac{1}{2}\widehat{DOF}=\frac{1}{2}sđ\widebat{DF}\)
Xét đt (O) có: \(\widehat{DEF}=\frac{1}{2}sđ\widebat{DF}\)(T/c góc nội tiếp) => \(\widehat{DOA}=\widehat{DEF}\)(1)
Ta có: AB,AC lần lượt là 2 tiếp tuyến của đt (O) (B,C là 2 tiếp điểm) (gt) => OA là tia phân giác của \(\widehat{BOC}\)(Định lý về 2 tiếp tuyến cắt nhau)
Lại có: OB = OC = R => \(\Delta OBC\)cân tại O (Đ/n) => OA vừa là phân giác đồng thời là đường cao của \(\Delta OBC\)(T/c của \(\Delta\)cân)=> \(OA\perp BC\)tại H (H là giao điểm của OA và BC)
Áp dụng hệ thức lượng trong \(\Delta\)vuông ABO (vuông tại B) với đường cao BH ta được: \(AB^2=AH.AO\)
Mà \(AB^2=AD.AE\left(cmt\right)\)=> \(AD.AE=AH.AO\Leftrightarrow\frac{AD}{AO}=\frac{AH}{AE}\)
Xét \(\Delta AHD\)và \(\Delta AEO\)có:
* \(\widehat{A}\)chung
* \(\frac{AD}{AO}=\frac{AH}{AE}\left(cmt\right)\)
=> \(\Delta AHD~\Delta AEO\left(c.g.c\right)\)=> \(\widehat{AHD}=\widehat{AEO}=\widehat{DEO}\left(Do\overline{A,D,E}\Rightarrow\widehat{AEO}=\widehat{DEO}\right)\)=> Tứ giác DEOH là tứ giác nội tiếp (Dhnb) => \(\widehat{DEH}=\widehat{DOH}=\widehat{DOA}\)(2 góc nội tiếp cùng chắn \(\widebat{DH}\)) (Do A,H,O => \(\widehat{DOH}=\widehat{DOA}\)) (2)
Từ (1) và (2) => \(\widehat{DEF}=\widehat{DEH}\)=> 3 điểm E,F,H thẳng hàng ( 2 góc cùng số đo, có 1 cạnh chung, 2 cạnh còn lại của 2 góc cùng nằm về 1 phía so với cạnh chung thì 2 cạnh còn lại trùng nhau) => Đpcm.

Lời giải:
Nói đơn giản thế này. Khi đề cho: Cho đồ thị hàm số $y=x+2$
- Hàm số: chính là $y=x+2$, biểu diễn mối quan hệ giữa biến $x$ và biến $y$. Hàm số hiểu đơn giản giống như phép biểu diễn mối quan hệ giữa hai biến.
- Đồ thị hàm số (hay đồ thị): Khi có hàm số rồi, người ta muốn biểu diễn nó trên mặt phẳng tọa độ ra được 1 hình thù nào đó thì đó là đồ thị hàm số. Ví dụ, đths $y=x+2$ có dạng như thế này:
- Tọa độ giao điểm của hai đồ thị: Khi ta vẽ được đồ thị trên mặt phẳng tọa độ, 2 đồ thị đó giao nhau ở vị trí nào thì đó chính là tọa độ giao điểm. Ví dụ, trên mp tọa độ ta có 2 đồ thị $y=-2x+3$ và $y=x+6$ chả hạn. Điểm $A$, có tọa độ $(-1,5)$ chính là giao điểm. Như vậy, $(-1,5)$ là tọa độ giao điểm.
- Nhìn hình vẽ của đồ thị chỉ giúp ta có cái nhìn trực quan hơn. Khi muốn tìm giao điểm của 2 đồ thị hàm số, người ta thường dùng hàm số để tìm cho nhanh, vì hàm số biểu diễn mối quan hệ giữa hai biến một cách "số hóa" hơn.
- Với nhiều hàm số trở lên thì ta cứ xét từng cặp 1 thôi.