Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Ta có DE là đường kính của (O)
\(\Rightarrow EF\perp DF\)
Mà \(DE\perp BC=K\Rightarrow\widehat{EKI}=\widehat{EFD}=90^0\)
=> DFIK nội tiếp
b ) Ta có :
\(AK\perp DE,EF\perp DF\)
\(\Rightarrow\widehat{AFE}=\widehat{AKE}=90^0\)
\(\Rightarrow AFKE\) nội tiếp
Mà IK = HK , \(DE\perp BC=K\) => DE là trung trực của HI
\(\Rightarrow\widehat{DHA}=\widehat{DHK}=\widehat{DIK}=\widehat{DFK}=\widehat{DEA}\)
c ) Ta có : \(\widehat{EIK}=\widehat{DAK}\)do AFKE nội tiếp
\(\widehat{AKD}=\widehat{EKI}=90^0\)
\(\Rightarrow\Delta AKD~\Delta EKI\left(g.g\right)\)
\(\Rightarrow\frac{AK}{EK}=\frac{KD}{KI}\)
\(\Rightarrow KE.KD=KI.AK\)
Lại có : \(\widehat{AFI}=\widehat{AKD}=90^0\Rightarrow\Delta AFI~\Delta AKD\left(g.g\right)\)
\(\Rightarrow\frac{AF}{AK}=\frac{AI}{AD}\Rightarrow AE.AD=AI.AK\)
Mà BCDF nội tiếp
\(\Rightarrow\widehat{AFB}=\widehat{ACD}\Rightarrow\Delta ABF~\Delta ADC\left(g.g\right)\)
\(\Rightarrow\frac{AF}{AC}=\frac{AB}{AD}\Rightarrow AF.AD=AB.AC\)
\(\Rightarrow AB.AC=AI.AK\)
=> KI.AB.AC = AI.AK.KI= AI.KE.KD

O N H E M D P
a) MN là tiếp tuyến đường tròn (O) \(\Rightarrow\widehat{MNP}=90^o\)
DO = ON = OP => \(DO=\frac{1}{2}NP\Rightarrow\widehat{NDP}=90^o\)
- Aps dụng hệ thức lượng cho tam giác MNP vuông tại N đường cao ND , ta có :
MN2 = MD . MP ( đpcm )
b) Ta có : PE // OM => PE // OH
Mà O là trung điểm của NP => OH là đường trung bình của tam giác ENP
=> H là trung điểm NE
Vậy : HN = HE ( đpcm )
c) Theo ( c/m câu b ) : HN = HE => \(HE\perp OM\)
Áp dung hệ thức trong tam giác NMO vuông tại N , đường cao NH :
Ta có : ON2 = OM . OH => OP2 = OM . OH
\(\Rightarrow\frac{OP}{OM}=\frac{OH}{OP}\left(1\right)\)
- Xét 2 tam giác: OHP và OPM
có : \(\frac{OP}{OM}=\frac{OH}{OP}\left(theo\left(1\right)\right)\)
\(\widehat{O}\)là góc chung
Do đó : \(\Delta OHP~\Delta OPM\left(c-g-c\right)\)
\(\Rightarrow\widehat{OPH}=\widehat{OMP}\left(đpcm\right)\)
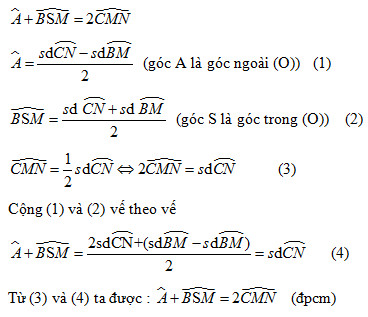
Điểm A nằm ngoài đường tròn (O) kẻ tiếp tuyến ABC vầ AMN, BN cắt CM tại S
Cmr
a, ^A+^BSM=2^CBN
b, AM. AN= AB.AC