Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng là
\(M\left( 6 \right) = 75 - 20\ln \left( {6 + 1} \right) = 36,08179702\)%.

Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:


Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là 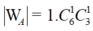 .
.
Vậy xác suất cần tính 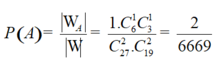 .
.
Chon C.

Điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam là tứ phân vị thứ ba.
Ta có: cỡ mẫu n = 35.
Tứ phân vị thứ ba \({Q_3}\) là \({x_{27}}\). Do \({x_{27}}\) đều thuộc nhóm \(\left[ {30;40} \right)\) nên nhóm náy chứa \({Q_3}\). Do đó,
\(p = 3;\;\;{a_3} = 30;\;\;{m_3} = 6;\;\;{m_1} + {m_2} = 4 + 19 = 23;\;{a_4} - {a_3} = 10\)
Ta có: \({Q_3} = 30 + \frac{{\frac{{3 \times 35}}{4} - 23}}{6} \times 10 = 35,42\).

a) Do số bệnh nhân là số nguyên nên ta hiệu chỉnh như sau:

Số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 là:
\(n = 7 + 8 + 7 + 6 + 2 = 30\).
Gọi \({x_1};{x_2};...;{x_{30}}\) là số bệnh nhân đến khám bệnh mỗi ngày được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_7} \in \begin{array}{*{20}{l}}{\left[ {0,5;10,5} \right)}\end{array};{x_8},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array};{x_{16}},...,{x_{22}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array};\\{x_{23}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{l}}{\left[ {40,5;50,5} \right)}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\)
Do \({x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array},{x_{16}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 20,5\).
• Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 30;{n_m} = 8;C = 7;{u_m} = 10,5;{u_{m + 1}} = 20,5\)
Do \({x_8} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{30}}{4} - 7}}{8}.\left( {20,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \({x_{23}}\).
Ta có: \(n = 30;{n_j} = 6;C = 7 + 8 + 7 = 22;{u_j} = 30,5;{u_{j + 1}} = 40,5\)
Do \({x_{23}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 30,5 + \frac{{\frac{{3.30}}{4} - 22}}{6}.\left( {40,5 - 30,5} \right) \approx 31,3\)
b) Do \({Q_3} \approx 31,3\) nên nhận định trên hợp lí.

Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.

Gọi A là biến cố “Người đó mắc bệnh tim”; B là biến cố “Người đó mắc bệnh huyết áp”; E là biến cố “Người đó không mắc cả bệnh tim và bệnh huyết áp”.
Khi đó \(\overline E \) là biến cố “Người đó mắc bệnh tim hoặc mắc bệnh huyết áp".
Ta có \(\overline E = A \cup B.\)
\(\begin{array}{l}P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = 8,2\% + 12,5\% - 5,7\% = 15\% \\ \Rightarrow P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - 15\% = 85\% \end{array}\)
Vậy tỉ lệ dân cư trên 50 tuổi của tỉnh X không mắc cả bệnh tim và bệnh huyết áp là 85%.



.png)



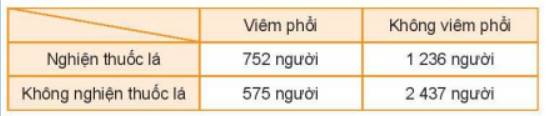
Chọn ngẫu nhiên một người đàn ông
Gọi A là biến cố “Người đó nghiện thuốc lá”, B là biến cố “Người đó mắc bệnh viêm phổi”
Khi đó, AB là biến cố “Người đó nghiện thuốc lá và mắc bệnh viêm phổi”
Ta có \(P\left( A \right) = \frac{{752 + 1236}}{{5000}} = \frac{{497}}{{1250}};P\left( B \right) = \frac{{752 + 575}}{{5000}} = \frac{{1327}}{{5000}}\)
\( \Rightarrow P\left( A \right).P\left( B \right) = \frac{{497}}{{1250}}.\frac{{1327}}{{5000}} = 0,10552304\)
Mặt khác \(P\left( {AB} \right) = \frac{{752}}{{5000}} = 0,1504\)
Vì \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) nên hai biến cố A và B không độc lập.
Vậy việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.