Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo em thì là hình b
Vì nó còn có thể phân chia mm nên dễ dàng đo đạc hơn.

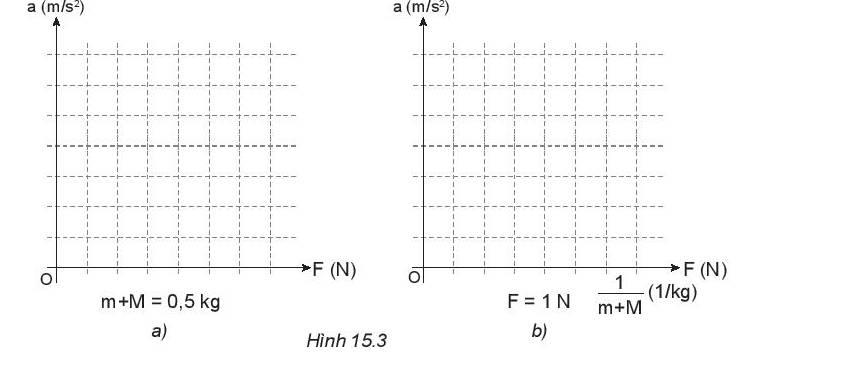
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
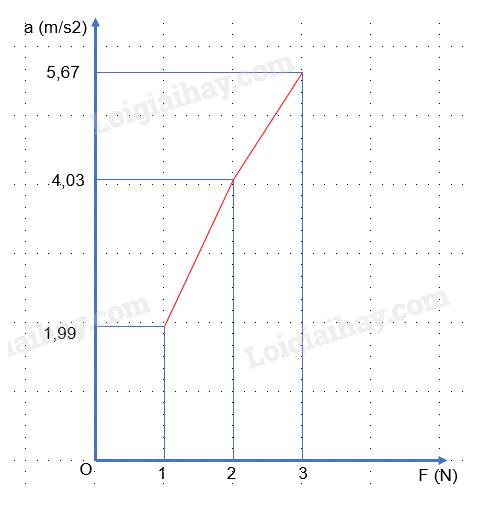
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
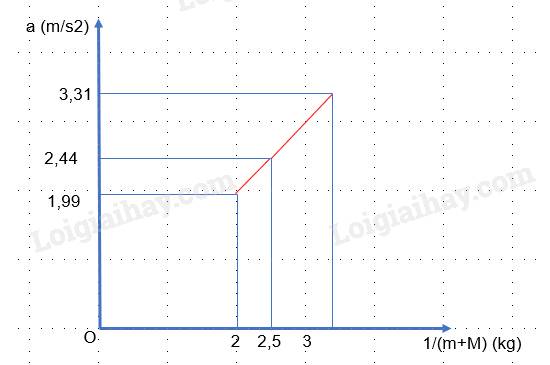
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

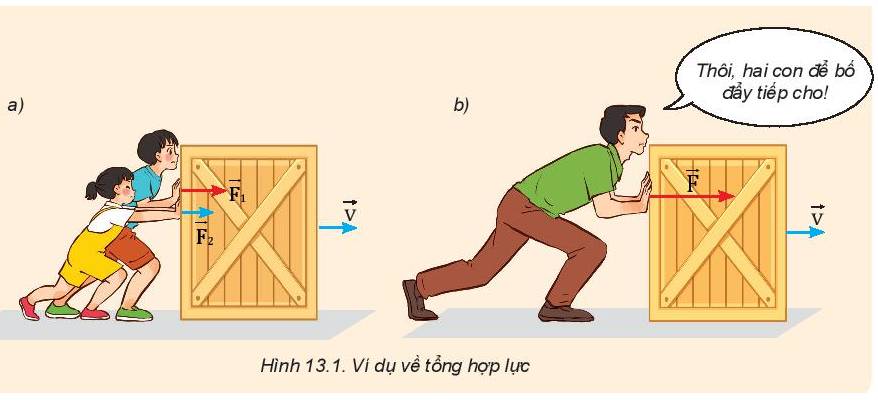
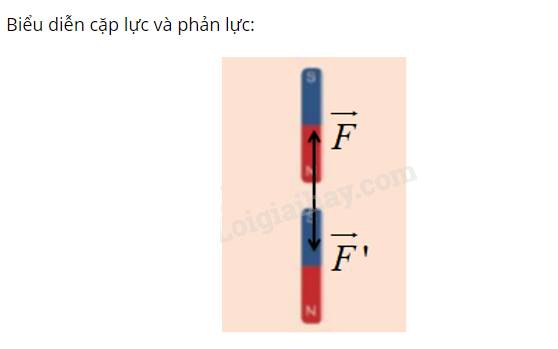
Lực đẩy của người bố trong hình có tác dụng như lực đẩy của hai anh em vì người bố khỏe, lực đẩy của bố bằng tổng lực đẩy của hai anh em cộng lại.

Sử dụng công thức tính trọng lực: \(P=m
.
g\)
Ta có:
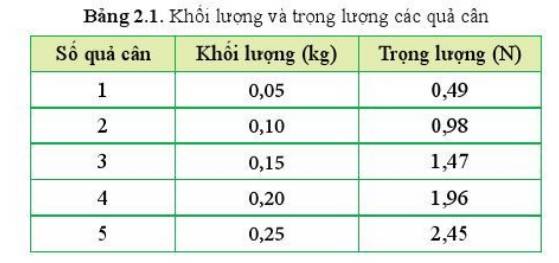
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)

1.
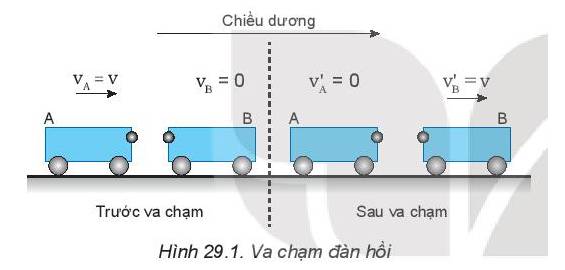
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_A' + m.v_B' = m.(v_A' + v_B') = m.\left( {\frac{v}{2} + \frac{v}{2}} \right) = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_A^{'2} + \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.\left( {\frac{{{v^2}}}{4} + \frac{{{v^2}}}{4}} \right) = \frac{1}{4}.m.{v^2}\)
2.
Từ kết quả câu 1, ta thấy trong va chạm mềm thì động lượng không thay đổi (được bảo toàn), động năng thay đổi (năng lượng không được bảo toàn).


Trọng lực có:
+ Điểm đặt tại trọng tâm của vật (quả táo).
+ Phương thẳng đứng.
+ Chiều từ trên xuống dưới.
+ Độ lớn phụ thuộc vào khối lượng của vật.

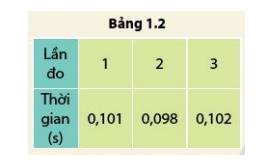
Thời gian trung bình của phép đo là:
\(\overline t = \frac{{{t_1} + {t_2} + {t_3}}}{3} = \frac{{0,101 + 0,098 + 0,102}}{3} \approx 0,100(s)\)
Sai số tuyệt đối trung bình của phép đo là:
\(\begin{array}{l}\Delta {t_1} = \left| {{t_2} - {t_1}} \right| = \left| {0,098 - 0,101} \right| = 0,003\\\Delta {t_2} = \left| {{t_3} - {t_2}} \right| = \left| {0,102 - 0,098} \right| = 0,004\\\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2}}}{2} = \frac{{0,003 + 0,004}}{2} \approx 0,004(s)\end{array}\)

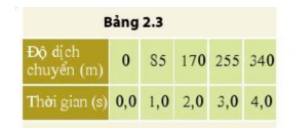
- Vẽ đồ thị độ dịch chuyển – thời gian: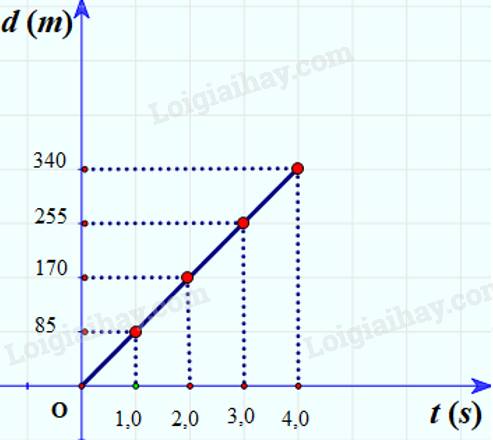
- Vận tốc của xe là:
\(v=\dfrac{d}{t}=85\left(m/s\right)\)
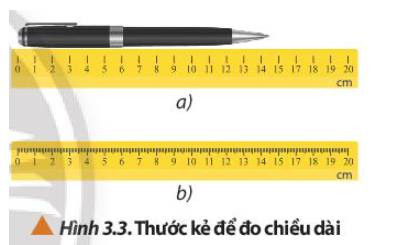
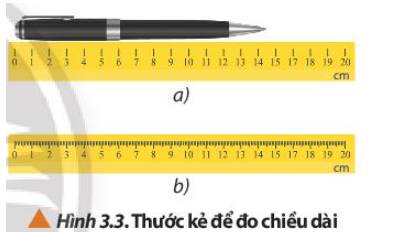



Để đo chiều dài của cây bút chì, nên sử dụng thước trong Hình 3.3b vì thước này có sai số dụng cụ nhỏ hơn thước ở Hình 3.3a nên kết quả đo sẽ chính xác hơn.