Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đo chiều dài của cây bút chì, nên sử dụng thước trong Hình 3.3b vì thước này có sai số dụng cụ nhỏ hơn thước ở Hình 3.3a nên kết quả đo sẽ chính xác hơn.

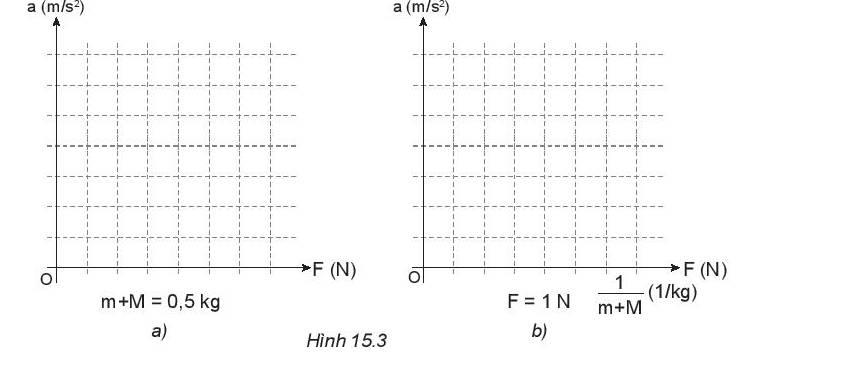
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
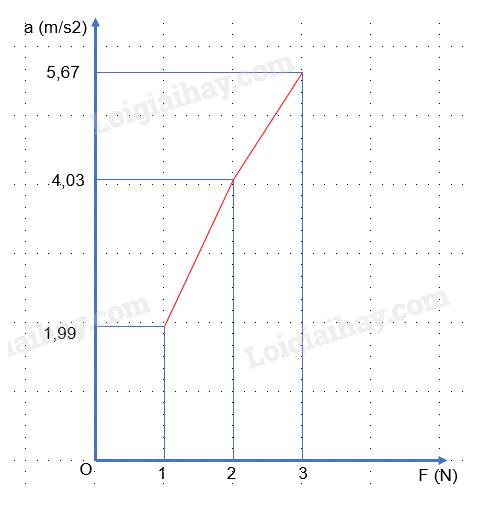
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
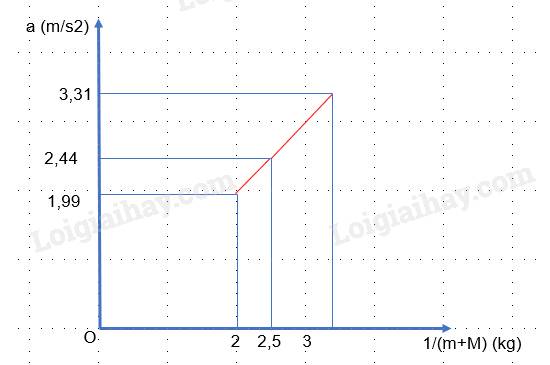
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

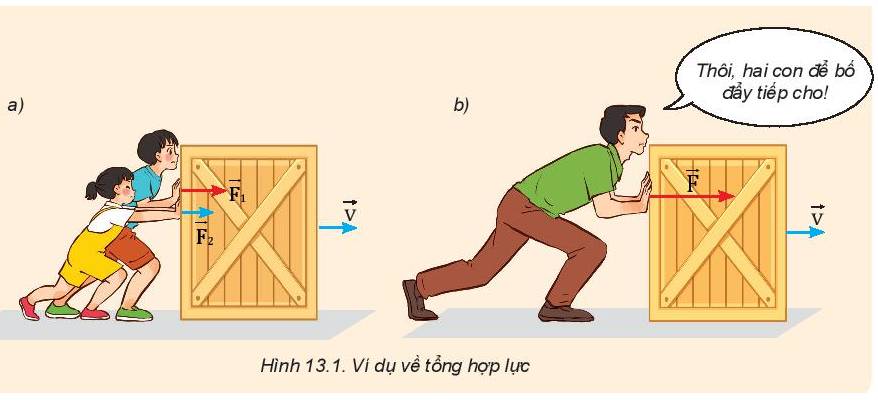
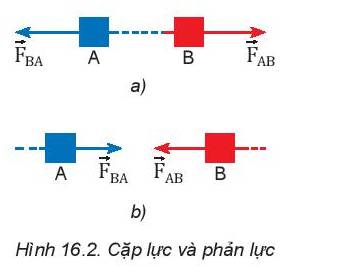
Lực đẩy của người bố trong hình có tác dụng như lực đẩy của hai anh em vì người bố khỏe, lực đẩy của bố bằng tổng lực đẩy của hai anh em cộng lại.

1.
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_A' + m.v_B' = m.(v_A' + v_B') = m.\left( {\frac{v}{2} + \frac{v}{2}} \right) = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_A^{'2} + \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.\left( {\frac{{{v^2}}}{4} + \frac{{{v^2}}}{4}} \right) = \frac{1}{4}.m.{v^2}\)
2.
Từ kết quả câu 1, ta thấy trong va chạm mềm thì động lượng không thay đổi (được bảo toàn), động năng thay đổi (năng lượng không được bảo toàn).

1. Giới hạn đo là số đo lớn nhất ghi trên dụng cụ.
⇒ Giới hạn đo của ampe kế ở hình 2.5 là 3A.
2. Nếu sử dụng ampe kế để đo dòng điện vượt quá giới hạn đo thì có thể làm cho ampe kế bị hư hỏng, thậm chí gây chập cháy.

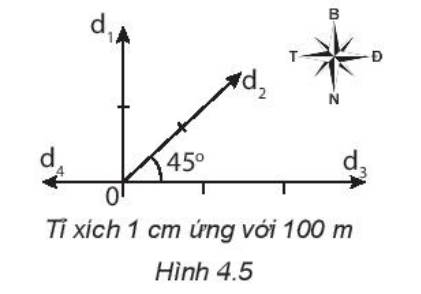
Độ dịch chuyển mô tả trên Hình 4.5 là:
+ d1 = 200 m (Bắc)
+ d2 = 200 m (Đông Bắc)
+ d3 = 300 m (Đông)
+ d4 = 100 m (Tây).

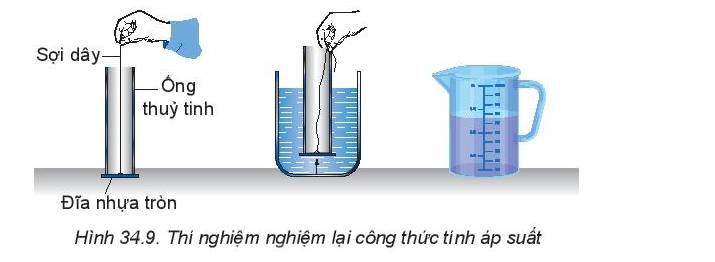
- Dùng dây kéo giữ miếng nhựa dính vào ống thủy tinh (hay nhựa) như ở hình a
- Nhúng ống thủy tinh có miếng nhựa vào nước rồi bỏ tay ra. Áp suất của chất lỏng tác dụng lên miếng nhựa giữ cho miếng nhựa không bị rơi xuống.
- Đổ từ từ nước trong cốc c vào ống. Khi mực nước trong ống ngang bằng hoặc lớn hơn một chút so với mực nước trong bình thì miếng nhựa rơi xuống.
- Lực của cột nước trong ống tác dụng lên miếng nhựa: \(P = mg = \rho gV = \rho gSh\) (1)
- Lực của nước trong bình tác dụng lên miếng nhựa: F = pS (2)
Vì P = F nên suy ra \(p = \frac{P}{S} = \rho gh\)

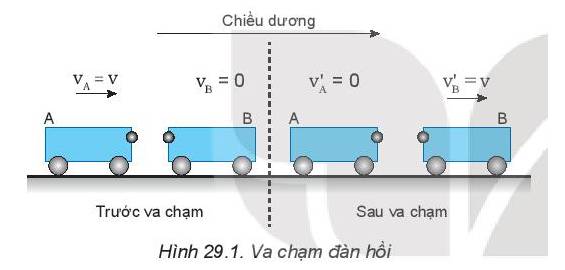
1.
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_B' = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.{v^2}\)
2.
Từ kết quả tính được, ta thấy trong va chạm đàn hồi, động lượng được bảo toàn, năng lượng được bảo toàn.
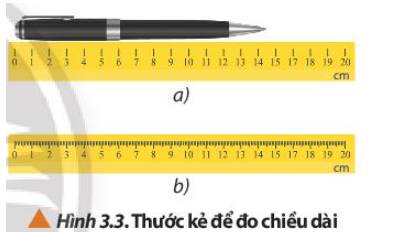
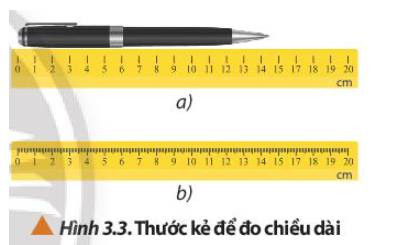



Theo em thì là hình b
Vì nó còn có thể phân chia mm nên dễ dàng đo đạc hơn.