Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

\(GTNN=\frac{1}{2}\left(17-\sqrt{67}\right)\Leftrightarrow x=\frac{7}{3}-\frac{\sqrt{67}}{3}\)

a:Ta có: \(A=-4x^2+x-1\)
\(=-4\left(x^2-\dfrac{1}{4}x+\dfrac{1}{4}\right)\)
\(=-4\left(x^2-2\cdot x\cdot\dfrac{1}{8}+\dfrac{1}{64}+\dfrac{63}{64}\right)\)
\(=-4\left(x-\dfrac{1}{8}\right)^2-\dfrac{63}{16}\le-\dfrac{63}{16}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{8}\)
b: Ta có: \(B=-3x^2+5x+6\)
\(=-3\left(x^2-\dfrac{5}{3}x-2\right)\)
\(=-3\left(x^2-2\cdot x\cdot\dfrac{5}{6}+\dfrac{25}{36}-\dfrac{97}{36}\right)\)
\(=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\le\dfrac{97}{12}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{6}\)
c: Ta có: \(C=-x^2+3x+4\)
\(=-\left(x^2-3x-4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{25}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)

\(2x^2+2y^2-4xy+2x-2y+4\)
\(=2\left(x-y\right)^2+2\left(x-y\right)+4\)
\(=2\left[\left(x-y\right)^2+2\left(x-y\right)\frac{1}{2}+\frac{1}{4}\right]+\frac{7}{2}\)
\(=2\left(x-y+\frac{1}{2}\right)^2+\frac{7}{2}\)
\(\Rightarrow A\ge\frac{7}{2}\)
Dấu = bn tự tính nhé

\(Q=x^2+y^2-4x-y+7\)
\(=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{11}{4}\)
\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x,y\)
Dấu '=' xảy ra khi x=2 và \(y=\dfrac{1}{2}\)

A = (2m-5)^2 -(2m+5)^2 +40m
= 4m^2 -20m+25 -(4m^2 +20m+25) + 40m
= 4m^2 -20m+25 -4m^2 -20m -25 + 40m
= 0.
Vậy biểu thức A ko phụ thuộc vào biến.
Bài 2:
Gọi 2 số nguyên liên tiếp là a và a+1 (a thuộc Z)
Ta có: (a+1)^2 -a^2
= a^2 +2a +1- a^2
= 2a+1
Mà 2a+1 là số lẻ nên (a+1)^2 -a^2 là số lẻ.
Vậy hiệu các bình phương của 2 số nguyên liên tiếp là số lẻ.
Bài 3:
P = (3x+4)^2 -10x- (x-4)(x+4)
= 9x^2 +24x +16 -10x - (x^2 -16)
= 9x^2 +24x +16 -10x -x^2 +16
= 8x^2 +14x +32
Bài 4:
Ta có: x^2 -4x+5
= (x^2 -4x+4)+ 1
= (x-2)^2 + 1
Vì (x-2)^2 >=0 với mọi x nên (x-2)^2 + 1 >=1 với mọi x.
Do đó: P = x^2 -4x+5 >=1 với mọi x.
Dấu "=" xảy ra khi: (x-2)^2 = 0
x-2 = 0
x = 2
Vậy GTNN của P là 1 tại x = 2.
Chúc bạn học tốt.

\(6,\\ a,\\ 1,A=x^2+3x+7=\left(x+\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{3}{2}\)
\(2,B=\left(x-2\right)\left(x-5\right)\left(x^2-7x+10\right)=\left(x-2\right)^2\left(x-5\right)^2\ge0\)
Dấu \("="\Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
\(b,\\ 1,A=11-10x-x^2=-\left(x+5\right)^2+36\le36\)
Dấu \("="\Leftrightarrow x=-5\)
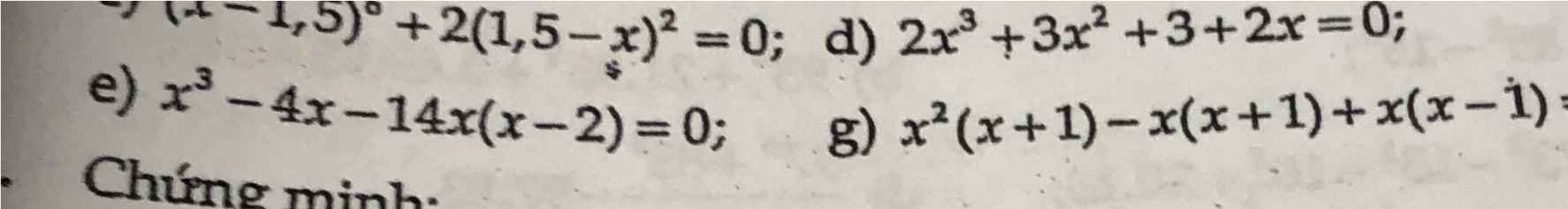
\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)