YK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1
A
22 tháng 6 2021
Ps : Bn tự vẽ hình nhé, mk chỉ giải thôi ạ.
a) Xét \(\Delta ABC\)và \(\Delta HAB\)
\(\widehat{BAC}=\widehat{BHA}=90^O\)
\(\widehat{ABC}chung\)
\(\Rightarrow\Delta ABC~\Delta HBA\)( g - g )
b) Xét \(\Delta AHD\)và \(\Delta CED\)
\(\widehat{AHD}=\widehat{CED}=90^O\)
\(\widehat{ADH}=\widehat{CDE}\)( đối đỉnh )
\(\Rightarrow\Delta AHD~\Delta CED\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AD}=\frac{CE}{CD}\Rightarrow AH.CD=AD.CE\)
c) Vì H là trung điểm của BD mà \(AH\perp BD\)
=> AH là đường trung trực của BD
\(\Rightarrow AB=AD\)
Mà : \(\frac{AH}{AD}=\frac{CE}{CD}\)
\(\Rightarrow\frac{AH}{AB}=\frac{CE}{CD}\)
Vì \(\Delta ABC~\Delta HBA\Rightarrow\frac{AH}{AB}=\frac{CA}{CB}\)
Do đó : \(\frac{CE}{CD}=\frac{CA}{CB}=\frac{8}{10}=\frac{4}{5}\)
Vì \(\Delta CED\)vuông
\(\Rightarrow S_{CED}=\frac{CE.ED}{2}\)
\(AB//FK\Rightarrow\widehat{BAH}=\widehat{KFH}\)
\(\widehat{AHB}=\widehat{FHK}=90^O\)
\(BA=HD\)
\(\Rightarrow\Delta AHB=\Delta FHK\)
\(\Rightarrow HA=HF\)mà \(CH\perp AF\)
=> CH là đường trung trực AF \(\Rightarrow\Delta ACF\)cân tại C
Do đó : D là trọng tâm \(\Delta ACF\)
\(\Rightarrow CD=\frac{2}{3}CH\)
Mà \(\cos ACB=\frac{AC}{BC}=\frac{CH}{CA}=\frac{4}{5}\Rightarrow CH=\frac{32}{5}\Rightarrow CD=\frac{64}{15}\)
\(\Rightarrow\frac{CE}{CD}=\frac{4}{5}\Rightarrow CE=\frac{256}{75}\)
\(ED=\sqrt{CD^2-CE^2}=\frac{64}{25}\)
\(\Rightarrow S_{CED}=\frac{8192}{1875}\)
d) Vì \(\Delta ACF\)cân tại C \(\Rightarrow KE//AF\Rightarrow\widehat{EKF}=\widehat{AFK}\)
Vì HK là trung tuyến \(\Delta AFK\)\(\Rightarrow\widehat{AFK}=\widehat{HKF}\)
Do đó : \(\widehat{HKF}=\widehat{EKF}\)
=> KD là phân giác \(\widehat{HKE}\)
# Aeri #
NQ
1
VT
30 tháng 12 2017
bài 113 nâng cao và các chuyên đề toán 8 đại số (Vũ Dương Thụy -Nguyễn Ngọc Đạm)
22 tháng 12 2016
a) ĐKXĐ: \(a^2-1\ne0\Rightarrow\left(a-1\right)\left(a+1\right)\ne0\Rightarrow a\ne\pm1\)
b) ta có \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{a^2-1}\)
\(=\frac{2a^2+a^2-a-a^2-a}{a^2-1}=\frac{2a^2-2}{a^2-1}=\frac{2\left(a^2-1\right)}{a^2-1}=2\)
2 tháng 8 2017
ĐK \(x\ne\left\{-2;2\right\}\)
a. Ta có \(A=\left(\frac{x}{\left(x+2\right)\left(x-2\right)}-\frac{2}{x-2}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
\(=\frac{x-2x-4+x-2}{\left(x+2\right)\left(x-2\right)}:\frac{x^2-4+10-x^2}{x+2}=-\frac{6}{\left(x-2\right)\left(x+2\right)}.\frac{x+2}{6}=-\frac{1}{x-2}\)
b. Ta có \(\left|x\right|=\frac{1}{2}\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
Với \(x=\frac{1}{2}\Rightarrow A=\frac{-1}{\frac{1}{2}-2}=\frac{2}{3}\)
Với \(x=-\frac{1}{2}\Rightarrow A=\frac{-1}{-\frac{1}{2}-2}=\frac{2}{5}\)
c. Để \(A< 0\Rightarrow-\frac{1}{x-2}< 0\Rightarrow x-2>0\Rightarrow x>2\)
Vậy với \(x>2\)thì \(A< 0\)
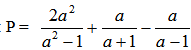
c) Ta có: \(C=7\left(x-8\right)^2-9\left(x+3\right)^2+50\)
\(=7\left(x^2-16x+64\right)-9\left(x^2+6x+9\right)+50\)
\(=7x^2-112x+448-9x^2-54x-81+50\)
\(=-2x^2-166x-31\)
\(=-2\cdot\dfrac{1}{49}-166\cdot\dfrac{-1}{7}-31\)
\(=\dfrac{-359}{49}\)
g) Ta có: \(G=x^{17}-3x^{16}+3x^{15}-3x^{14}+...+3x\)
\(=x^{17}-x^{16}\left(x+1\right)+x^{15}\left(x+1\right)-x^{14}\left(x+1\right)+...+x\left(x+1\right)\)
\(=x^{17}-x^{17}-x^{16}+x^{16}+x^{15}-x^{15}-x^{14}+...+x^2+x\)
=x
=2