Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Trên dây có sóng dừng với hai bụng sóng nên
![]() .
.
M, N thuộc hai bó sóng liên tiếp nên ngược pha nhau.
Khoảng cách MN nhỏ nhất khi M, N ở vị trí cân bằng hay
![]() .
.
Gọi trung điểm MN là O (khi đó chính là một nút) thì OM = 4cm = λ/6.
Vậy biên độ dao động của M và N là:
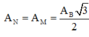 (vì M và N đối xứng nhau qua nút biên độ dao động bằng nhau).
(vì M và N đối xứng nhau qua nút biên độ dao động bằng nhau).
Khoảng cách M, B lớn nhất là
![]() khi M, N nằm ở biên.
khi M, N nằm ở biên.
Mặt khác
![]()
![]() .
.

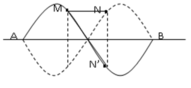
+ Trên dây có 2 bụng sóng nên: λ = 2 l k = 2.24 2 = 24 cm
+ Khi dây duỗi thẳng thì M, N chia dây làm 3 đoạn bằng nhau nên: AM = MN = NB = 8 cm.
+ MNmin = MN = 8 cm.
+ MNmax = MN’ = 8 2 + N N ' 2
® M N max M N min = 64 + N N ' 2 8 = 1 , 25 ® NN’ = 6 cm.
® A b ung = 2 3 cm
ü Đáp án C

Đáp án C
+ A, B là nút sóng, trên dây AB có bụng sóng ⇒ λ = l = 24 c m
+ M, N là hai điểm trên dây chia thành 3 đoạn bằng nhau khi dây duỗi thẳng → M, N cách nút sóng gần đó nhất đoạn λ 6 = 4 c m
⇒ A M = A N = A b sin 2 π . λ 6 λ = 3 c m
+ M, N thuộc hai bó liên tiếp nhau nên dao động ngược pha với nhau.
+ Khoảng cách MN nhỏ nhất khi sợi dây duỗi thẳng M N min = A B 3 = 8 c m
+ Khoảng cách MN lớn nhất khi M, N cùng đến biên:
M N max = A B 3 2 + A M + A M 2 = 10 c m
+ Vậy δ = M N max M N min = 10 8 = 1 , 25

Đáp án C
+ Khi xuất hiện sóng dừng, trên dây có hai bụng sóng → sóng dừng trên dây với hai bó sóng → λ = 24cm → M và N lần lượt cách nút gần nhất một đoạn λ/6 = 4 cm.
A N = A M = A b 3 2 = 2 3 3 2 = 3 cm .
+ M và N thuộc hai bó sóng liên tiếp nên dao động ngược pha nhau → MN lớn nhất khi M và N cùng đến biên, MN nhỏ nhất khi M và N cùng đến biên, MN nhỏ nhất khi M, N cùng đi qua vị trí cân bằng.
→ σ = MN 2 + ( 2 A N ) 2 MN 2 = 8 2 + 6 2 8 2 = 1 , 25 .

Đáp án D
M và N nằm trên hai bó sóng liên tiếp sẽ dao động ngược pha nhau
+ Khoảng cách giữa M và N nhỏ nhất khi M và N cùng đi qua vị trí cân bằng theo hai chiều ngược nhau d min = λ 3 = 8 cm
+ Khoảng cách giữa M và N lớn nhất khi M và N đang ở vị trí biên d m a x = 1 , 25 d min = 1 , 25.8 = 10 cm
Từ hình vẽ ta có d m a x = 2 A M 2 + d min 2 → A M = 3 cm
+ M cách bụng gần nhất một đoạn λ 6 → A M = 3 2 A = 2 3 cm

Đáp án A
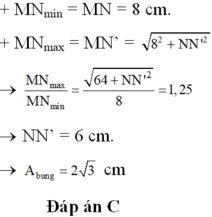
+ Với M, N, P, Q là các điểm cách đều nhau và dao động với cùng biên độ → Các điểm này chỉ có thể là bụng sóng cách nhau nửa bước sóng hoặc các điểm dao động với biên độ 2 2 A b cách nhau một phần tám bước sóng.
→ Trường hợp M, N, P và Q là các bụng sóng → A B = 4 λ 2 = 32 c m → λ = 16 cm.
+ M, Q thuộc hai bó sóng đối xứng nhau qua một nút sóng nên dao động ngược pha nhau.
→ M Q m i n tương ứng với M và Q cùng đi qua vị trí cân bằng theo hai chiều ngược nhau, M Q m a x tương ứng với M ở biên dương và Q ở biên âm.
Ta có tỉ số M Q m a x M Q min = 24 2 + 10 2 24 = 13 12
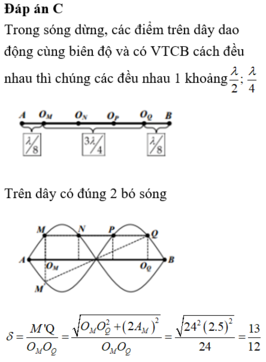
→ Trường hợp M, N, P và Q là các điểm dao động với biên độ bằng 2 2 A b → A B = 2 λ 2 = 32 cm → λ = 32 cm.
+ M, Q thuộc hai bó sóng đối xứng nhau qua một nút sóng nên dao động ngược pha nhau.
→ M Q m i n tương ứng với M và Q cùng đi qua vị trí cân bằng theo hai chiều ngược nhau, M Q m a x tương ứng với M ở biên dương và Q ở biên âm.
Ta có tỉ số M Q m a x M Q min = 24 2 + 10 2 24 = 13 12


M N P Q 4 4
Bước sóng: \(\lambda=24cm\)
Biên độ tại một điểm cách nút khoảng d là: \(a=A\sin\frac{2\pi d}{\lambda}\), trong đó A là biên độ của bụng sóng.
Khi dao động tại M đến P, tại N đến Q thì khoảng cách 2 điểm là max, khi ở VTCB thì khoảng cách min.
Tỉ số khoảng cách max, min giữa M và N là: \(\frac{PQ}{MN}=1,25\)
\(\Rightarrow\frac{\sqrt{4^2+a^2}}{4}=1,25\Rightarrow a=3cm\)
Mà: \(a=A\sin\frac{2\pi d}{\lambda}=A\sin\frac{2\pi.4}{24}=A\frac{\sqrt{3}}{2}=3\Rightarrow A=2\sqrt{3}cm\)
Vậy biên độ dao động của bụng là: \(2\sqrt{3}cm\)