Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ud Uc Um 120V 120V 45 45
Từ giản đồ véc tơ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
Cường độ dòng điện của mạch \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}A\)
Công suất tiêu thụ cuộn dây: \(P=U.I\cos\varphi=120.0,6\sqrt{2}\cos45^0=72W\)

Ta có: $U_{Lr-C}= U \dfrac{\sqrt{r^2 + (Z_L-Z_C)^2}}{\sqrt{(R+r)^2 + (Z_L-Z_C)^2}}.$
Do đó, theo tính chất hàm số:
$f(Z_C)=\dfrac{r^2 + (Z_L-Z_C)^2}{(R+r)^2 + (Z_L-Z_C)^2}.$
Ta có hàm số đạt cực tiểu khi $Z_C=Z_L.$
Ta tìm được:
$C=\dfrac{10^{-3}}{4 \pi} F.$
Thay vào biểu thức trên ta được:
$U_{min}=120.$

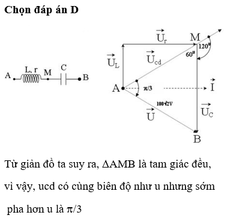
Ta có Ud=UC Mà ta có \(_{ }\varphi_d\)=π/4 ..Từ hình vẽ thấy : cos \(\varphi_d\)= \(\frac{\sqrt{2}}{2}=\frac{U_r}{U_d}\) → Ur=\(\frac{1}{\sqrt{2}}\)Ud
Có U2= Ud2+ Ud2 -- 2 Ud.Ud.cos 45 → U= Ud.\(\sqrt{2-\sqrt{2}}\)
Hình vẽ → cos\(\varphi_m\)= \(\frac{Ur}{U}\)= \(\frac{\frac{1}{\sqrt{2}}}{\sqrt{2-\sqrt{2}}}\) = 0,924
Ud Uc=Ud UL Ur U
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm một cuộn dây mắc nối tiếp với một tụ
điện. Điện áp hiệu dụng giữa hai đầu cuộn dây có giá trị bằng điện áp hiệu dụng giữa hai bản tụ điện.
Dòng điện tức thời trong đoạn mạch chậm pha pi/4 so với điện áp tức thời giữa 2 đầu cuộn dây. Hệ số công suất của đoạn mạch là
A. 0,707. B. 0,866. C. 0,924. D. 0,999.
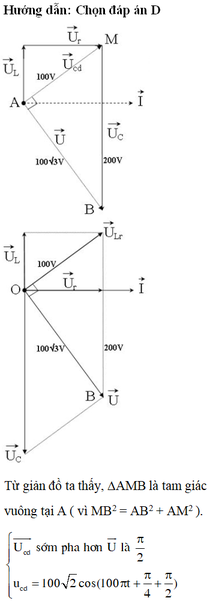
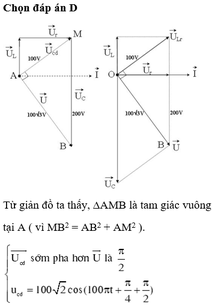
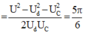

i Ud Uc U 100 200V 100can3
Nhận xét: \(200^2=100^2+\left(100\sqrt{3}\right)^2\)
Nên u vuông pha với ud như hình vẽ.
\(\Rightarrow\varphi_d=\varphi_u+\frac{\pi}{2}=\frac{\pi}{4}+\frac{\pi}{2}=\frac{3\pi}{4}\)
Biểu thức điện áp hai đầu cuộn dây: \(u=100\sqrt{2}\cos\left(100\pi t+\frac{3\pi}{4}\right)\)
điện xoay chiều à