Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do quả bóng tiếp xúc với các mặt của hình lập phương
\(\Rightarrow S=a\) với a là cạnh hình lập phương
Ta có \(V=a^3\Rightarrow a=\sqrt[3]{V}=\sqrt[3]{8000}=20\left(cm\right)\)
\(\Rightarrow S=2o\left(cm\right)\)

Gọi a là cạnh hình lập phương
Suy ra bán kính hình cầu là 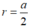
Diện tích toàn phần của hình lập phương : S 1 = 6 a 2 (đvdt)
Diện tích của hình cầu là:
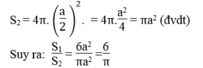

Nếu bán kính hình cầu là 4cm thì cạnh hình lập phương là 8cm
Thể tích hình lập phương :
V 1 = 8 3 = 512 ( c m 3 )
Thể tích hình cầu là :
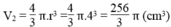
Vậy thể tích phần trống trong hình hộp và ngoài hình cầu là:
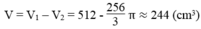

Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Một quả bong tennis có dạng hình cầu, người ta đo được chu vi của dường tròn bao quanh quả bóng là 20,41cm. Vậy một đựng bóng tennis cao 19,5cm có thể chứa nhiều nhất bao nhiêu quả bóng ten-nít? lớp 5 help tui

1 R=0,5 1 1
Thể tích khối lập phương là : 1^3=1 (m^3)
Thể tích lượng nước tran ra chính bằng thể tích khối chóp được đặt vào:
Thể tích khối chóp là:
\(\frac{1}{3}\pi R^2h\)=\(\frac{1}{3}.\pi.0,5^2.1=\frac{\pi}{12}\left(m^3\right)\)
Vậy tỉ số cần tìm là: \(\frac{\pi}{12}:1=\frac{\pi}{12}\)
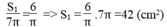
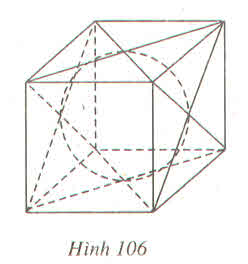
ta có
V=8000cm^3
=> Cạnh của hình lập phương là 8000cm
mà quả bóng tx vs các mặt hlp nên đg kính quả bóng=cạnh hlp
=>đk bóng là 8000cm
hok tốt
thank!