Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

lời này là mik ăn copy của bn
lời 2 : hai chân ta đá í a trái banh
đá qua đá lại banh lăn xuống phố đến hồi đi kiếm trái banh mất tiêu i i i i i i là trò chơi banh i i i chơi tình tính tang tang là trò chơi banh i i i i i i ~ MÚN CHƠI LỜI NÀO CX ĐƯỢC >_< vô đối ~

Ta đi, đi khắp í a quê hương, hát lên hát một câu ca thắm thiết : Nước mình đẹp quá có nơi nào bằng ? Ngàn hoa thắm tươi trên đường rộn ràng kìa muôn cánh chim tung hoành trời đất bao la nào anh nào em ta hãy hát vang lên nào !!!
Ra sân đá bóng í a với nhau. Đá qua, đá lại, đá lên đá xuống mãi chẳng vào lưới í a quả nào... Ì i í i i trò, là trò đá bóng, í i i trò, tình tính tang tang là trò, là trò đá bóng í i í i....
Em đi chơi vs í a bạn bè.Giấu cha dấu mẹ chân đi khé né miệng cười khe khẽ lén mẹ đi chơi iii chốn là chốn đi chơi iiiii chốn tình tính tang tang là chốn là chốn đi chơi iiiiii


Lời giải
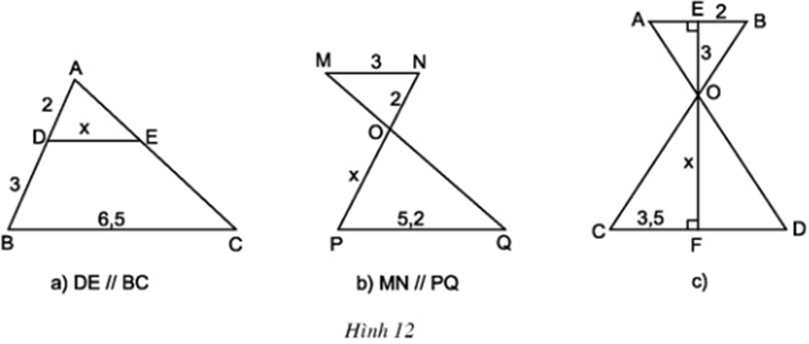
Áp dụng định lí Ta – lét ta có:
- Hình a:
- Hình b:
- Hình c:
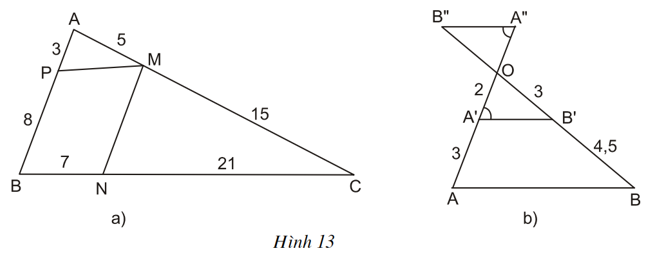
Bài 6 (trang 62 SGK Toán 8 tập 2): Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Lời giải:
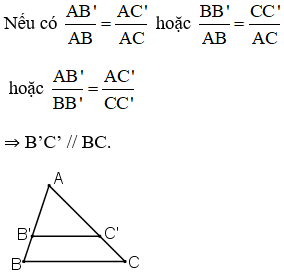
a) Xét hình 13a) : MN // AC.
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có:
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
Vậy ta có AB//A’B’//A”B”.
Kiến thức áp dụng
Định lý Ta-let đảo :
+ Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
ΔABC, B’ ∈ AB, C’ ∈ AC.

bạn thử xem nhũng dạng này nhé (huyện tớ là thế k biết huyện bạn cấu trúc đề có như thế k)
1, phân tích đa thức thành nhân tử
2. tính gt của đa thức
3. CM đẳng thức, bất đẳng thức
4. tính chia hết đối với số nguyên
5. tính chia hết đối với đa thức
6. tìm GTNN,GTLN
7,SÔ nguyên tố
8, hình học
bạn cũng thi hsg toán à.........bắt tay đc k?
tớ cũng thế nhưng chưa thi
OoO Min min OoO: bt hả
có nhiều dạng lắm, nếu cần nhắn tin đi rồi tớ chỉ, hừm, 28 thi ròi à,tớ thi xong rồi, chúc bạn thi tốt và giành đc giải cao nha

H A B O x y
Gọi \(A\left(x;y\right)\). Do \(A,B\in\left(E\right)\) có hoành độ dương và tam giác \(OAB\) cân tại \(O\), nên:
\(B\left(x;y\right),x>0.=>AB=2\left|y\right|=\sqrt{4-x^2}\)
Gọi \(H\) là trung điểm \(AB,\) ta có: \(OH\pm AB\) và \(OH=x\).
Diện tích: \(S_{OAB}=\frac{1}{2}x\sqrt{4-x^2}\)
\(=\frac{1}{2}\sqrt{x^2\left(4-x^2\right)\le1}\)
Dấu " = " xảy ra, khi và chỉ khi \(x=\sqrt{2}\)
Vậy: \(A\left(\sqrt{2};\frac{\sqrt{2}}{2}\right)\) và \(B\left(\sqrt{2};-\frac{\sqrt{2}}{2}\right)\) hoặc \(A\left(\sqrt{2};-\frac{\sqrt{2}}{2}\right)\) và \(B\left(\sqrt{2};\frac{\sqrt{2}}{2}\right)\).
O 2 2 A y x
Phương trình chính tắc của \(\left(E\right)\) có dạng: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), với \(a>b>0\) và \(2a=8=>a=4\).
Do \(\left(E\right)\) và \(\left(C\right)\) cùng nhận \(Ox\) và \(Oy\) làm trục đối xứng và các giao điểm là các đỉnh của một hình vuông nên \(\left(E\right)\) và \(\left(C\right)\) có một giao điểm với tọa độ dạng \(A\left(t;t\right),t>0\)
\(A\in\left(C\right)\Leftrightarrow t^2+t^2=8=>t=2\)
\(A\left(2;2\right)\in\left(E\right)\Leftrightarrow\frac{4}{16}+\frac{4}{b^2}=1\Leftrightarrow b^2=\frac{16}{3}\)
Phương trình chính tắc của \(\left(E\right)\) là \(\frac{x^2}{16}+\frac{y^2}{\frac{16}{3}}=1\)
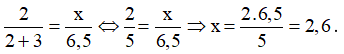
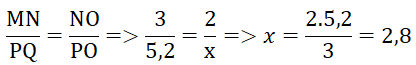
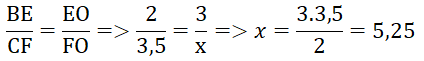
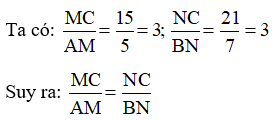
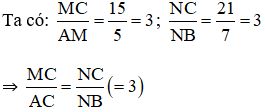
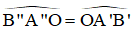
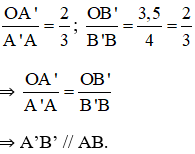
nghe xem câu hát của tôi thế nào ?hát ca múa nhạy tôi đây thíh nhất hát hoài chẳng lo tối hơi chút nào[/QUOTE][/QUOTE]
tình tang tính tang tang tình là hò câu hát của tôi đầy này
hò cóng sênh sênh là hò là câu hát í i ì i í i
Vậy thì bn làm câu hỏi của mk đi