K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 4 2020
Gọi H là trung điểm AO \(\Rightarrow HM\) là đường trung bình tam giác SAO
\(\Rightarrow\left\{{}\begin{matrix}HM//SO\\HM=\frac{1}{2}SO\end{matrix}\right.\) \(\Rightarrow HM\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{MNH}\) là góc giữa MN và (ABCD) \(\Rightarrow\widehat{MNH}=60^0\)
\(NH=\sqrt{\left(\frac{3a}{4}\right)^2+\left(\frac{a}{4}\right)^2}=\frac{a\sqrt{10}}{4}\)
\(\Rightarrow MH=NH.tan60^0=\frac{a\sqrt{30}}{4}\)
\(SO=2MH=\frac{a\sqrt{30}}{2}\)
\(MN=\frac{NH}{cos60^0}=\frac{a\sqrt{10}}{2}\)
b/ Gọi E; F lần lượt là trung điểm AB; AD \(\Rightarrow EF//BD\) \(\Rightarrow\left(MEF\right)//\left(SCD\right)\Rightarrow\) góc giữa MN và (SBD) bằng góc giữa MN và (MEF)
\(EN//AC\) (do EN là đường trung bình tam giác ABC)
Mà \(AC\perp\left(SBD\right)\Rightarrow AC\perp\left(MEF\right)\Rightarrow EN\perp\left(MEF\right)\)
\(\Rightarrow\widehat{NME}\) là góc giữa NM và (MEF)
\(EN=\frac{AC}{2}=\frac{a\sqrt{2}}{2}\)
\(\Rightarrow sin\widehat{NME}=\frac{EN}{MN}=\frac{\sqrt{5}}{5}\Rightarrow\widehat{NME}\approx26^033'\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2022
a.
\(y'=\left(x^2\right)'-\left(cosx\right)'=2x-\left(-sinx\right)=2x+sinx\)
b.
\(y'=\left(3sinx\right)'+\left(2cosx\right)'=3cosx+\left(-2sinx\right)=3cosx-2sinx\)
c.
\(y'=\left(5cos\left(2x-\dfrac{\pi}{4}\right)\right)'=5\left(2x-\dfrac{\pi}{4}\right)'.\left(-sin\left(2x-\dfrac{\pi}{4}\right)\right)=-10sin\left(2x-\dfrac{\pi}{4}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2019
\(\left(x+2.x^{-2}\right)^6=\sum\limits^6_{k=0}C_6^kx^k.2^{6-k}.\left(x^{-2}\right)^{6-k}=\sum\limits^6_{k=0}C_6^k2^{6-k}x^{3k-12}\)
Số hạng chứa \(x^3\Rightarrow3k-12=3\Rightarrow k=5\)
\(\Rightarrow\) Hệ số: \(C_6^5.2^1=12\)
\(\left(3-2x\right)^{15}=\sum\limits^{15}_{k=0}C_{15}^k3^k.\left(-2\right)^{15-k}.x^{15-k}\)
Số hạng chứa \(x^7\Rightarrow15-k=7\Rightarrow k=8\)
\(\Rightarrow\) Hệ số: \(C_{15}^8.3^8.\left(-2\right)^7\)
\(\left(2x-x^{-2}\right)^6=\sum\limits^6_{k=0}C_6^k2^k.x^k.\left(-1\right)^{6-k}.\left(x^{-2}\right)^{6-k}=\sum\limits^6_{k=0}C_6^k2^k\left(-1\right)^{6-k}.x^{3k-12}\)
Số hạng ko chứa x \(\Rightarrow3k-12=0\Rightarrow k=4\)
Hệ số: \(C_6^42^4\left(-1\right)^2=240\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2+ax-2}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{ax-2}{\sqrt{x^2+ax-2}+x}=\lim\limits_{x\rightarrow+\infty}\dfrac{a-\dfrac{2}{x}}{\sqrt{1+\dfrac{a}{x}-\dfrac{2}{x^2}}+1}=\dfrac{a}{2}\)
\(\Rightarrow\dfrac{a}{2}=1\Rightarrow a=2\in\left(1;3\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
17.
Hàm có đúng 1 điểm gián đoạn khi và chỉ khi: \(x^2-2\left(m+3\right)x+9=0\) có đúng 1 nghiệm
\(\Rightarrow\Delta'=\left(m+3\right)^2-9=0\)
\(\Leftrightarrow m^2+6m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-6\end{matrix}\right.\)
\(\Rightarrow0+\left(-6\right)=-6\)
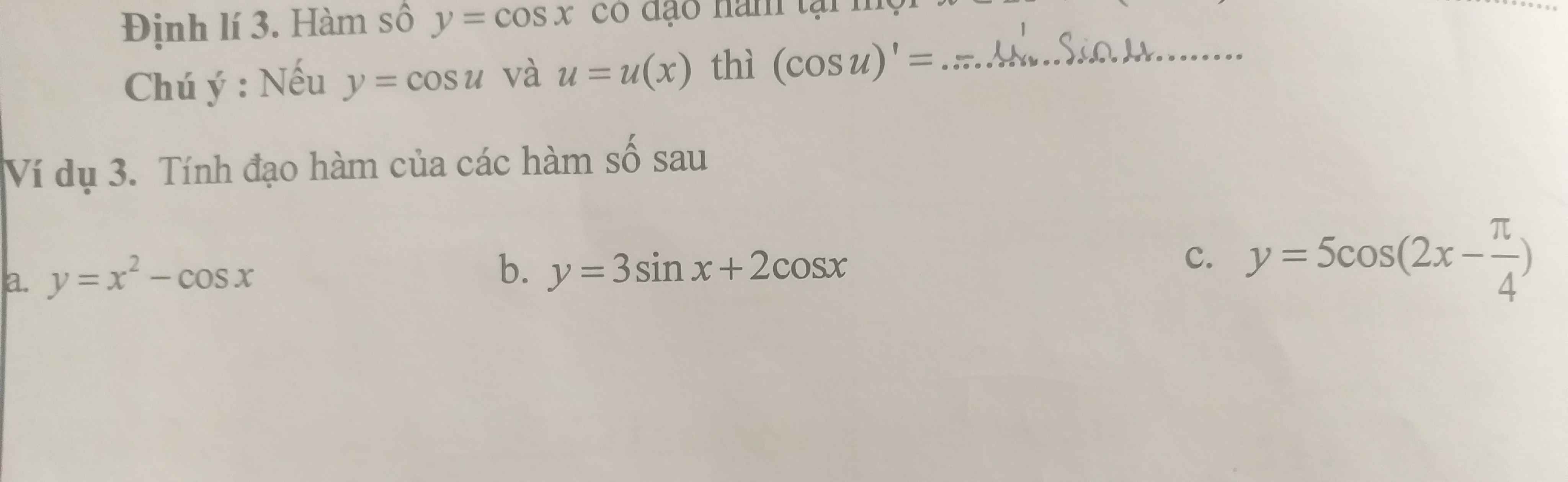
a: Trong mp(SBC), gọi M là giao điểm của SO với BC
Chọn mp(SBC) có chứa SO
\(SO\subset\left(SBC\right);SO\subset\left(SAO\right)\)
Do đó: (SBC) giao (SAO)=SO
Vì M là giao điểm của CB với SO
nên M là giao điểm của CB với mp(SAO)
b: Gọi N là giao điểm của AC và BD
\(N\in AC\subset\left(SAC\right)\)
\(N\in BD\subset\left(SBD\right)\)
Do đó: \(N\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SN
c: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
d: AB//CD
CD\(\subset\)(SCD)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)