Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1 ,2 mỗi đề í
có 4 đề thì mỗi đề chỉ càn làm bài 1 , bài 2 hoi ..
bạn có thể làm cho mình đc hông ạ

Ta có: \(A=\frac{1}{2}-\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{98}-\frac{1}{99}\)
\(\Rightarrow A=\frac{1}{6}+\frac{1}{20}+.....+\frac{1}{9702}\)
\(\Rightarrow A=\frac{1}{2.3}+\frac{1}{4.5}+...+\frac{1}{98.99}\)
\(\Rightarrow A=\frac{1}{2}-\frac{1}{99}\)
\(\Rightarrow A=\frac{97}{198}\)


bài 3:
tổng số giờ đã chảy đc từ 2 vòi : 1+1=2(giờ)
tổng số phần bể đã chảy được từ 2 vòi : \(\dfrac{1}{5}+\dfrac{1}{7}=\dfrac{7}{35}+\dfrac{5}{35}=\dfrac{12}{35}\left(ph\text{ần} b\text{ể}\right)\)
nếu chảy cùng lúc mỗi giờ chảy được : \(\dfrac{12}{35}:2=\dfrac{12}{35\cdot2}=\dfrac{6}{35}\left(ph\text{ần}b\text{ể}\right)\)
bài 4:
cách 1:
độ dài đoạn AB là : \(\dfrac{3}{4}+\dfrac{9}{8}=\dfrac{18}{24}+\dfrac{27}{24}=\dfrac{45}{24}\left(m\right)\)
diện tích ABCD là : \(\dfrac{45}{27}\cdot\dfrac{4}{7}=\dfrac{15}{14}\left(m^2\right)\)
cách 2:
diện tích AEFD là : \(\dfrac{3}{4}\cdot\dfrac{4}{7}=\dfrac{3}{7}\left(m^2\right)\)
diện tích EBCF là : \(\dfrac{9}{8}\cdot\dfrac{4}{7}=\dfrac{9}{14}\left(m^2\right)\)
diện tích ABCD là : \(\dfrac{3}{7}+\dfrac{9}{14}=\dfrac{15}{14}\left(m^2\right)\)


Cs phải cái đề như này ko e : 6,5 - 4/9 : | x/4 + 1/3 | = 2 ( dấu ":" dấu chia )

Bài 3:
Số học sinh kém là:
40-8-10-20=2(bạn)
Tỉ số phần trăm giữa số học sinh giỏi so với lớp là:
8:40=20%
Tỉ số phần trăm giữa số học sinh khá so với lớp là:
20:40=50%
Tỉ số phần trăm giữa số học sinh trung bình so với lớp là:
10:40=25%
Tỉ số phần trăm giữa số học sinh yếu so với lớp là:
2:40=5%






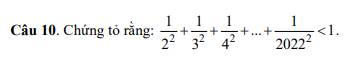
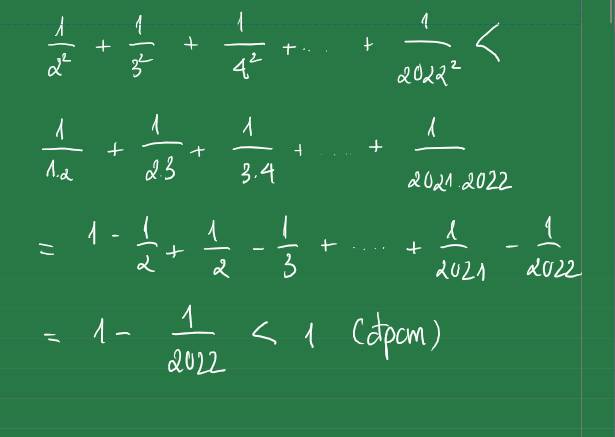
\(S=\dfrac{1}{1!}+\dfrac{1}{2!}+....+\dfrac{1}{2001!}\)
\(S=1+\dfrac{1}{2!}+\dfrac{1}{3!}+.....+\dfrac{1}{2001!}\)
\(\dfrac{1}{2!}=\dfrac{1}{1\times2};\dfrac{1}{3!}< \dfrac{1}{2\times3};...;\dfrac{1}{2001!}< \dfrac{1}{2000\times2001}\)
\(\dfrac{1}{2!}+\dfrac{1}{3!}+....+\dfrac{1}{2001!}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+....+\dfrac{1}{2000\times2001}\)
\(S< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2000}-\dfrac{1}{2001}\)
\(S< 2-\dfrac{1}{2001}< 2< 3\)
=> \(S< 3\)