Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TH1: m=-1
BPT sẽ là:
-2(-1-1)x-3-3>0
=>4x-6>0
=>x>6/4
=>Loại
TH2: m<>-1
Δ=(2m-2)^2-4(m+1)(3m-3)
=4m^2-8m+4-4(3m^2-3)
=4m^2-8m+4-12m^2+12
=-8m^2-8m+16
Để BPT vô nghiệm thì -8m^2-8m+16<=0 và m+1<0
=>m^2+m-2>=0 và m<-1
=>(m+2)(m-1)>=0 và m<-1
=>(m>=1 hoặc m<=-2) và m<-1
=>m<=-2
Đáp án D.
Ta có:
P T ⇔ m 9 4 x - 2 m + 1 6 4 x + m ≤ 0
⇔ m 3 2 2 x - 2 m + 1 3 2 x + m ≤ 0
Đ ặ t t = 3 2 x ; d o x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .
Khi đó PT trở thành:
m t 2 - 2 m + 1 t + m ≤ 0 ⇔ m t 2 - 2 t + 1 ≤ t
Rõ ràng t =1 là nghiệm của BPT đã cho.
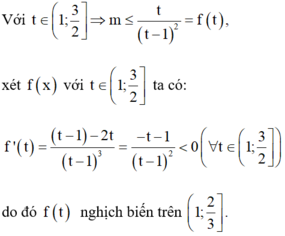
D o đ ó B P T n g h i ệ m đ ú n g v ớ i ∀ t ∈ 1 ; 3 2
⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6 .
Vậy có 6 giá trị nguyên dương của m thỏa mãn.
Chọn C
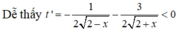
nên hàm t = t (x) nghịch biến trên (-2;2)
Thay vào bất phương trình trên được:
Bất phương trình đã cho nghiệm đúng với mọi x ∈ - 2 ; 2 nếu và chỉ nếu bất phương trình
nghiệm đúng với mọi t ∈ - 6 ; 2
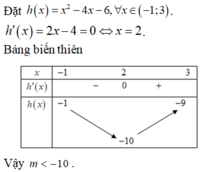
tam thức bậc hai f t = 2 t 2 - m t + 3 m - 5 có hai nghiệm thỏa mãn
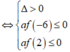
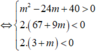
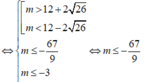
Kết hợp với m ∈ - 10 ; 10 thì m ∈ - 10 ; - 9 ; - 8
\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên
Chọn C.
Bất phương trình
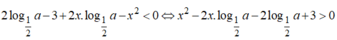
Đặt ,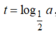 
khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
Bất phương trình (*) nghiệm đúng với mọi x khi và chỉ khi
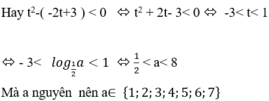
Vậy có tất cả 7 giá trị nguyên của a thỏa mãn yêu cầu bài toán.
Câu 1:
\(\Leftrightarrow x^2-4x+5+\sqrt{x^2-4x+5}-5=m\)
Đặt \(\sqrt{x^2-4x+5}=\sqrt{\left(x-2\right)^2+1}=a\ge1\)
\(\Rightarrow a^2+a-5=m\) (1)
Xét phương trình: \(x^2-4x+5=a^2\Leftrightarrow x^2-4x+5-a^2=0\)
\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=5-a^2\end{matrix}\right.\)
\(\Rightarrow\) Nếu \(5-a^2>0\Rightarrow1\le a< \sqrt{5}\) thì pt có 2 nghiệm dương
Nếu \(5-a^2\le0\) \(\Leftrightarrow a\ge\sqrt{5}\) thì pt có 1 nghiệm dương
Vậy để pt đã cho có đúng 2 nghiệm dương thì: (1) có đúng 1 nghiệm thỏa mãn \(1\le a< \sqrt{5}\) hoặc có 2 nghiệm pb \(a_1>a_2\ge\sqrt{5}\)
Xét \(f\left(a\right)=a^2+a-5\) với \(a\ge1\)
\(f'\left(a\right)=0\Rightarrow a=-\frac{1}{2}< 1\Rightarrow f\left(a\right)\) đồng biến \(\forall a\ge1\) \(\Rightarrow y=m\) chỉ có thể cắt \(y=f\left(a\right)\) tại nhiều nhất 1 điểm có hoành độ \(a\ge1\)
\(f\left(1\right)=-3\) ; \(f\left(\sqrt{5}\right)=\sqrt{5}\)
\(\Rightarrow\) Để pt có 2 nghiệm pb đều dương thì \(-3\le m< \sqrt{5}\)
Câu 2:
\(x^2-3x+2\le0\Leftrightarrow1\le x\le2\) (1)
Ta có: \(mx^2+\left(m+1\right)x+m+1\ge0\)
\(\Leftrightarrow m\left(x^2+x+1\right)\ge-x-1\)
\(\Leftrightarrow m\ge\frac{-x-1}{x^2+x+1}=f\left(x\right)\) (2)
Để mọi nghiệm của (1) là nghiệm của (2) \(\Leftrightarrow\left(2\right)\) đúng với mọi \(x\in\left[1;2\right]\)
\(\Rightarrow m\ge\max\limits_{\left[1;2\right]}f\left(x\right)\)
\(f'\left(x\right)=\frac{-\left(x^2+x+1\right)+\left(2x+1\right)\left(x+1\right)}{\left(x^2+x+1\right)^2}=\frac{x^2+2x}{\left(x^2+x+1\right)^2}>0\) \(\forall x\in\left[1;2\right]\)
\(\Rightarrow f\left(x\right)\) đồng biến \(\Rightarrow\max\limits_{\left[1;2\right]}f\left(x\right)=f\left(2\right)=-\frac{3}{7}\)
\(\Rightarrow m\ge-\frac{3}{7}\)
\(\Leftrightarrow\dfrac{3^x+3}{\sqrt{9^x+1}}=m\)
Đặt \(3^x=t>0\)
\(\Rightarrow\dfrac{t+3}{\sqrt{t^2+1}}=m\)
Xét hàm \(f\left(t\right)=\dfrac{t+3}{\sqrt{t^2+1}}\) khi \(t>0\) rồi lập BBT, từ đó xác định ra m có vẻ khá đơn giản
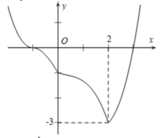
Đặt \(\frac{3}{5}=cosa;\frac{4}{5}=sina\)
\(f\left(x\right)=5.sin\left(x+a\right)-\left(m^3-4m+3\right)x-m+5\)
Dễ dàng nhận thấy \(f\left(x\right)\) là hàm liên tục
- Nếu \(m^3-4m+3\ne0\)
Khi \(m>0\Rightarrow\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\infty\); \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 lần đổi dấu trên R \(\Rightarrow f\left(x\right)=0\) có nghiệm
Tương tự, khi \(m< 0\Rightarrow f\left(+\infty\right)=-\infty\) ; \(f\left(-\infty\right)=+\infty\) nên \(f\left(x\right)=0\) có nghiệm
\(\Rightarrow\) Phương trình vô nghiệm khi và chỉ khi \(\left\{{}\begin{matrix}m^2-4m+3=0\\m>0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=\frac{-1+\sqrt{13}}{2}\end{matrix}\right.\)