
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



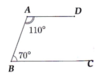
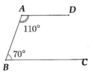
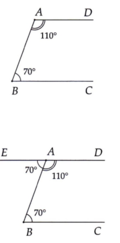
a) Ta có D A B ^ + A B C ^ = 180°.
Mà hai góc ở vị trí trong cùng phía.
Từ đó AD // BC (tính chất hai đường thẳng song song).
b) Cách 1:
E A B ^ + B A D ^ = 70° + 110° = 180°
Cách 2: E A B ^ = A B C ^ = 70°
Mà hai góc ở vị trí so le trong nên AE// BC ( tính chất hai đường thẳng song song)
Lại có AD//BC ( chứng minh ý a)) nên Ad = AE.
Vậy E, A, D thẳng hàng

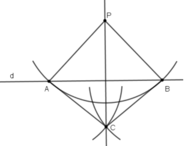
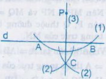
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
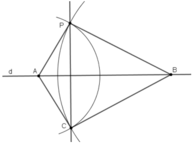
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.

Gọi giao điểm của AB và xy là O
\( \Rightarrow \) O là trung điểm AB (Do xy là đường trung trực của AB)
\( \Rightarrow \) Đo khoảng cách AO và từ điểm O kẻ OB sao cho OA = OB và nằm khác phía với điểm A so với đường thẳng xy (A, B, O thẳng hàng)

có 3 cách bạn ạ
C1 : chứng minh 1 góc bằng 180 độ
C2: coi như 3 điểm đó chưa thẳng hàng ta tách ra làm 2 đoạn chẳng hạn AC và CB. Gọi d là một đường thẳng ko giao hay cx ko trùng với một trong 2 đoạn AC, CB . Cần Chứng minh AC//d Cb//d là đk vì khi đó AC, Cb trùng nhau suy ra A<B<C thẳng hàng
C3 : Chứng minh điểm nằm giữa là trung điểm của đoạn thẳng tạo bởi 2 điểm còn lại

1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác .
8. Sử dụng tính chất hình bình hành.
9. Sử dụng tính chất góc nội tiếp đường tròn.
10. Sử dụng góc bằng nhau đối đỉnh
11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng
12. Chứng minh phản chứng
13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0
14. Sử dụng sự đồng qui của các đường thẳng.
nếu mk làm sai thì cho mk xin lỗi,nếu đúng thì h cho mk mha


14 phương pháp chứng minh 3 điểm thẳng hàng
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác .
8. Sử dụng tính chất hình bình hành.
9. Sử dụng tính chất góc nội tiếp đường tròn.
10. Sử dụng góc bằng nhau đối đỉnh
11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng
12. Chứng minh phản chứng
13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0
14. Sử dụng sự đồng qui của các đường thẳng.
Thật ra, chứng minh thẳng hàng có hàng tá cách, nhưng mỗi bài toán chỉ có từ 2 - 3 cách giải (nếu theo như lượng kiến thức đang học). Vì vậy, mình chỉ liệt kê ra một, hai cái thôi nhé:
+ Theo tiên đề Ơclit, qua một điểm nằm ngoài đường thẳng chỉ kẻ được một và duy nhất một đường thẳng đi qua điểm đó và song song với đường thẳng đã cho. Nếu có thể kẻ được 2 đường thì 2 đường thẳng đó trùng nhau. Như vậy chúng thẳng hàng.
+ Chứng minh ba điểm thẳng hàng tạo thành hai góc kề bù.
+ Chứng minh vuông góc.
+ Ba điểm cùng nằm trên các đường trong tam giác.