Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


14 = 2 .7 nên phân số 5 14 viết được dưới dạng số thập phân vô hạn tuần hoàn.
20 = 2 2 .5nên phân số 1 20 viết được dưới dạng số thập phân hữu hạn.
35 75 = 1 25 có 25 = 5 2 nên phân số 35 75 viết được dưới dạng số thập phân hữu hạn.
- 11 - 100 = 11 100 có 100 = 2 2 . 5 2 nên phân số - 11 - 100 viết được dưới dạng số thập phân hữu hạn.
6 15 = 2 5 có 5 = 5 nên phân số 6 15 viết được dưới dạng số thập phân hữu hạn.
Như vậy, trong năm phân số 5 14 ; 1 20 ; 35 75 ; 6 15 có một phân số viết được dưới dạng số thập phân vô hạn tuần hoàn.
Đáp án cần chọn là: A

Ta có: \(n\left(n+1\right)\left(n+2\right)\) chia hết cho 3.
=> \(\frac{52}{n\left(n+1\right)\left(n+2\right)}\) là stp hữu hạn.

Ta thấy 45 = 3 2 .5 ; 18 = 2. 3 2 nên các phân số 2 7 ; 2 45 ; - 7 18 đều viết được dưới dạng số thập phân vô hạn tuần hoàn.
Phân số - 5 - 240 = 1 48 có 48 = 2 4 .3 nên phân số - 5 - 240 viết được dưới dạng số thập phân vô hạn tuần hoàn.
Như vậy cả bốn phân số 2 7 ; 2 45 ; - 5 - 240 ; - 7 18 đều viết được dưới dạng số thập phân vô hạn tuần hoàn.
Đáp án cần chọn là: D

Ta thấy
45
=
3
2
.
5
;
18
=
2
.
3
2
nên các phân số 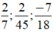 được viết dưới dạng số thập phân vô hạn tuần hoàn.
được viết dưới dạng số thập phân vô hạn tuần hoàn.
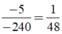 có
48
=
2
4
.
3
nên phân số -5/-240 được viết dưới dạng số thập phân vô hạn tuần hoàn.
có
48
=
2
4
.
3
nên phân số -5/-240 được viết dưới dạng số thập phân vô hạn tuần hoàn.
Vậy có 4 phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.
Chọn đáp án D.

Thử lấy ví dụ 2 số thập phân vô hạn tuần hoàn ta có:
\(0,\left(37\right)=\frac{37}{99}\)
\(0,\left(62\right)=\frac{62}{99}\)
=> 0,(37)+0,(62)=\(\frac{37}{99}+\frac{62}{99}=1\)
Vì 1 là số tự nhiên
=> Tổng của 2 số thập phân vô hạn tuần hoàn có thể là số tự nhiên