Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
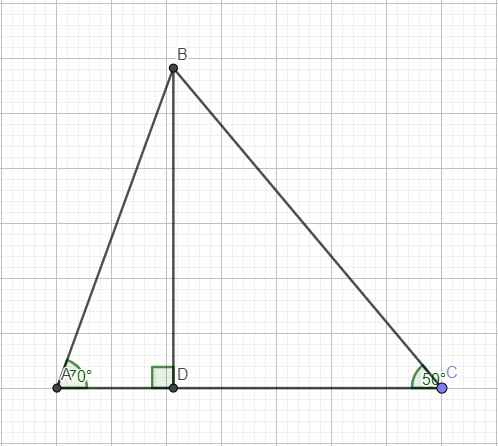
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)

Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
cosC=HC/AC⇒HC=cosC.AC=cos50.35≈22cm
⇒AH=√AC^2−HC^2=√35^2−22^2=√741cm
Trong tam giác vuông AHB ta có:
sinB=AH/AB⇒AB=AH/sinB=√741/sin60=2√247cm
⇒HB=√AB^2−AH^2=√(2√247)^2−741=√247cm
Vậy SABC=AH(HB+HC)/2=√741.(√247+22)/2≈513\(cm^2\)

Tối thiểu em phải ghi đúng đề ra chứ. Đường cao là đường cao nào? H là điểm nào? Đó là những chi tiết trong đề còn thiếu

A B C H 2,5
Xét tam giác ABH vuông tại H( AH là đường cao) có:
\(AH=AB.sinB\Rightarrow AB=\frac{AH}{sinB}=\frac{2,5}{sin60^o}=\frac{5\sqrt{3}}{3}\left(cm\right)\)
Xét tam giác ACH vt H (AH là đường cao) có:
\(AH=AC.sinC\Rightarrow AC=\frac{AH}{sinC}=\frac{2,5}{sin40^o}\approx3,9\left(cm\right)\)
Lại có:
+) \(\Delta ABH\) vt H => BH=AH.cot B = 2,5 . cot 60o=\(\frac{5\sqrt{3}}{6}\)(cm)
+) \(\Delta ACH\) vt H => CH=AH.cot C = 2,5 . cot 40o\(\approx3\)(cm)
=> \(BC=BH+CH\approx\frac{5\sqrt{3}}{6}+3\approx4,44\)(cm)

[ACD] = [ABCD] - [ABC] = 35,3554 cm2
kẻ BH _|_ AC ; DK_|_ AC cắt MN tại P
=> \(k=\frac{DP}{DK}=\frac{DP}{DK}-1+1=\frac{PK}{DK}+1=\frac{BH}{DK}+1=\frac{\left[ABC\right]}{\left[ACD\right]}+1=1,4399978504\)
[DMN]=k2 .[ADC] = .....tự tính nhé
B2