Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không mất tính tổng quát, giả sử toa 1 có đúng 4 hành khách. Khi đó số cách để các hành khách lên toa 1 là \(C^4_8=70\) cách. Nếu gọi \(x,y\) lần lượt là số hành khách trên toa 2, 3 thì \(\left(x,y\right)\in\left\{\left(4;0\right);\left(3;1\right);\left(2;2\right);\left(3;1\right);\left(4;0\right)\right\}\). Khi đó có tất cả \(2\left(C^0_4+C^3_4.C^1_1\right)+C^2_4.C^2_2=16\) (cách). Vậy có tất cả là \(3.70.16=3360\) cách thỏa ycbt \(\Rightarrow\) Chọn C

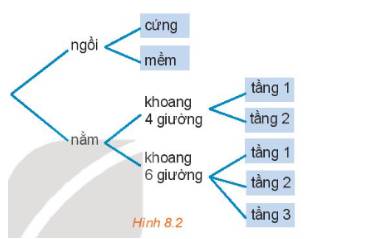
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)

Có tổng cộng 6 cách là:
1 ng thuộc tổ 1 và 1 ng thuộc tổ 2
1 ng thuộc tổ 1 và 1 ng thuộc tổ 3
1 ng thuộc tổ 1 và 1 ng thuộc tổ 4
1 ng thuộc tổ 2 và 1 ng thuộc tổ 3
1 ng thuộc tổ 2 và 1 ng thuộc tổ 4
1 ng thuộc tổ 3 và 1 ng thuộc tổ 4

Số cách xếp là:
\(C^2_3\cdot6\cdot1\cdot5=90\left(cách\right)\)

Coi 8 cuốn sách toán như 1 cuốn
=>Cần xếp 13 cuốn vào 13 vị trí khác nhau
=>Có 13! cách
Số cách xếp 8 cuốn sách toán là 8!(cách)
Số cách xếp là \(13!\cdot8!\)(cách)

Gọi x là số phòng 3 người, y là số phòng 2 người, z là số phòng 1 người, ta được hệ phương trình
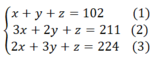
Cách 1. Dùng máy tính cầm tay.
Cách 2. Khử z để đưa về hệ phương trình hai ẩn. Trừ vế theo vế phương trình (2) cho phương trình (1) và phương trình (2) cho phương trình (3) ta được hệ phương trình
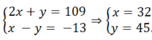
Từ đó thay vào (1) ta được z = 25.
Vậy đáp án là B.
Cách 3. Tính nhẩm.
Với phương án A, vế trái của phương trình (2) bằng 243 nên bị loại. Với phương án C, vế trái của phương trình (3) bằng 245 nên bị loại. Tương tự với phương án D, vế trái của phương trình (3) bằng 245 nên loại.
Đáp án: B
Số cách xếp là:
\(C^3_4\cdot5\cdot1\cdot4=80\left(cách\right)\)