Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
(a - b) - (b + c) + (c - a) - (a - b - c)
= a - b - b - c + c - a - a + b + c
= (a - a) + (b - b) + (c - c) - (a + b - c)
=0 + 0 + 0 - (a + b - c)
= - (a + b - c) (đpcm)
2. chju
P = a . ( b - a ) - b . ( a - c ) - bc
P = ab - a2 - ba + bc - bc
P = ab - a2 - ba
P = a . ( b - a - b )
P = a . ( - a ) mà a khác 0 => P có giá trị âm
Vậy biểu thức P luôn âm với a khác 0

Không. Vì không có phân số nào mà cả tử số và mẫu số nhân với hai số khác nhau lại bằng phân số đã cho cả (hay do m khác n)

a. VT:(x-y)-(x-z)
= x-y-x+z
= z-y
VP:(z+x)-(y+x)
=z+x-y-x
=z-y
=> VT=VP => đpcm.
b. VT:(x-y+z)-(y+z-x)-(x-y)
= x-y+z-y-z+x-x+y
= x-y
VP:(z-y)-(z-x)
= z-y-z+x
= x-y
=> VT=VP => đpcm.
c. VT: a(b+c)-b(a-c)
=ab+ac-ab+bc
= ac+bc
VP: (a+b)c
= ac+bc
=> VT=VP => đpcm.
d. VT: a(b-c)-a(b+d)
= ab-ac-ab-ad
= -ac-ad
VP: -a(c+d)
= -ac-ad
=> VT=VP => đpcm
tương tự...

Ta có:
Mà a = b + c nên
Từ (1), (2) suy ra:
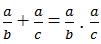

giả sử điều phải chứng minh là đúng thì:
\(\dfrac{\left(a+c\right)^2}{\left(a-c\right)^2}=\dfrac{\left(b+d\right)^2}{\left(b-d\right)^2}\\ \Rightarrow\left[\left(a+c\right)\left(b-d\right)\right]^2=\left[\left(a-c\right)\left(b+d\right)\right]^2\\ \Leftrightarrow\left(ab+bc-ad-cd\right)^2=\left(ab+ad-bc-cd\right)^2\\ \Leftrightarrow\left(ab+bc-ad-cd\right)^2-\left(ab+ad-bc-cd\right)^2=0\\ \Leftrightarrow\left(ab+bc-ad-cd+ab+ad-bc-cd\right)\left(ab+bc-ad-cd-ab-ad+bc+cd\right)=0\\ \Leftrightarrow\left(2ab-2cd\right)\left(2bc-2ad\right)=0\\ \Leftrightarrow\left(ab-cd\right)\left(bc-ad\right)=0\\ \Rightarrow\left[{}\begin{matrix}ab-cd=0\\bc-ad=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}ab=cd\\bc=ad\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{a}{c}=\dfrac{d}{b}\\\dfrac{a}{b}=\dfrac{c}{d}\left(đúng\right)\end{matrix}\right.\)
do đó điều phải chứng minh là đúng

a,a-b+c-d=a+c-b-d=(a+c)-(b+d)(đpcm)
b,(a-b)-(c-d)=a-b-c+d=(a+d)-(b+c)(đpcm)
a, Ta có (a-b) +(c-d) = a-b+c-d = (a+c)-(b+d) ( ĐPCM)
b, Ta có (a-b)-(c-d) = a-b-c+d = ( a+d) - ( b+c) ( ĐPCM )
Tk mk nhé

Ta có : \(\frac{a}{b}=\frac{c}{d}\)
Nên \(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
Suy ra : \(\frac{a}{c}=\frac{a-b}{c-d}\)
Vậy : \(\frac{a-b}{a}=\frac{c-d}{c}\)
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)=>a=bk,c=dk
a,Ta có \(\frac{a-b}{a}-\frac{bk-b}{bk}=\frac{b\left(k-1\right)}{bk}\frac{k-1}{k}.1\)
Tương tự ta có \(\frac{c-d}{c}=\frac{k-1}{k}.2\)
Từ (1) và (2) suy ra đều phải chứng minh .
b,Ta có \(\frac{a+b}{c+d}=\frac{bk+b}{dk+d}=\frac{b\left(k+1\right)}{d\left(k+1\right)}=\frac{b}{d}.3\)
Tương tự ta có \(\frac{a-b}{c-b}=\frac{b}{d}.4\)
Từ (3) và (4) suy ra đều phải chứng minh
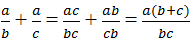
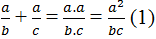
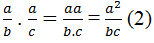
Đâu chia hết cho 2 đâu.
a=b=c=d=1 thì sao chia hết cho 2?