Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=9\)
Ta có : VT = \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
\(\Leftrightarrow VT=9\) \(=VP\)
Vậy.........
b) \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
<=> \(\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2=6\)
Ta có : VT = \(2+\sqrt{3}+2-\sqrt{3}+2\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
= \(4+2\sqrt{4-3}=4+2=6\)
=> VT = VP
Vậy.....
c) \(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=8\)
Ta có : VT = \(\dfrac{\sqrt{4}}{\sqrt{\left(2-\sqrt{5}\right)^2}}-\dfrac{\sqrt{4}}{\sqrt{\left(2+\sqrt{5}\right)^2}}\)
= \(\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{2+\sqrt{5}}=\dfrac{4+2\sqrt{5}-2\sqrt{5}+4}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
= \(\dfrac{8}{5-4}=8\)
=> VT = VP
Vậy....
a) Biến đổi vế trái ta có:
VT= \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}\)
= \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
= 9 = VP
Vậy đẳng thức đc chứng minh
b) Đặt vế trái = A = \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
\(A^2=\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2\)
\(A^2=2+\sqrt{3}+2-\sqrt{3}+2.\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(A^2=4+2.\sqrt{4-3}=4+2.1=6\)
\(\Rightarrow A=\sqrt{6}=VP\)
Vậy đẳng thức đc chứng minh

a) VT=\left(\dfrac{2 \sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right) \cdot \dfrac{1}{\sqrt{6}}VT=(8−223−6−3216)⋅61
=\left(\dfrac{\sqrt{2} \cdot \sqrt{2} \cdot \sqrt{3}-\sqrt{6}}{\sqrt{2^{2} \cdot 2}-2}-\dfrac{\sqrt{6^{2} .6}}{3}\right) \cdot \dfrac{1}{\sqrt{6}}=(22⋅2−22⋅2⋅3−6−362.6)⋅61
=\left(\dfrac{\sqrt{2} \cdot \sqrt{6}-\sqrt{6}}{2 \sqrt{2}-2}-\dfrac{6 . \sqrt{6}}{3}\right) \cdot \dfrac{1}{\sqrt{6}}=(22−22⋅6−6−36.6)⋅61
=\left[\dfrac{\sqrt{6}(\sqrt{2}-1)}{2(\sqrt{2}-1)}-\dfrac{6 \sqrt{6}}{3}\right] \cdot \dfrac{1}{\sqrt{6}}=[2(2−1)6(2−1)−366]⋅61
=\left(\dfrac{\sqrt{6}}{2}-2 \sqrt{6}\right) \cdot \dfrac{1}{\sqrt{6}}=(26−26)⋅61
=\left(\dfrac{\sqrt{6}}{2}-\dfrac{4 \sqrt{6}}{2}\right) \cdot \dfrac{1}{\sqrt{6}}=(26−246)⋅61
=\left(\dfrac{-3}{2} \sqrt{6}\right) \cdot \dfrac{1}{\sqrt{6}}=(2−36)⋅61
=-\dfrac{3}{2}=-1,5=V P=−23=−1,5=VP.
b) VT=\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right): \dfrac{1}{\sqrt{7}-\sqrt{5}}VT=(1−214−7+1−315−5):7−51
=\left(\dfrac{\sqrt{7} \cdot \sqrt{2}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{5} \cdot \sqrt{3}-\sqrt{5}}{1-\sqrt{3}}\right): \dfrac{1}{\sqrt{7}-\sqrt{5}}=(1−27⋅2−7+1−35⋅3−5):7−51
=\left[\dfrac{\sqrt{7}(\sqrt{2}-1)}{1-\sqrt{2}}+\dfrac{\sqrt{5}(\sqrt{3}-1)}{1-\sqrt{3}}\right]: \dfrac{1}{\sqrt{7}-\sqrt{5}}=[1−27(2−1)+1−35(3−1)]:7−51
=(-\sqrt{7}-\sqrt{5})(\sqrt{7}-\sqrt{5})=(−7−5)(7−5)
=-(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})=−(7+5)(7−5)
=-(7-5)=-2=VP=−(7−5)=−2=VP.
c) V T=\dfrac{a \sqrt{b}+b \sqrt{a}}{\sqrt{a b}}: \dfrac{1}{\sqrt{a}-\sqrt{b}}VT=abab+ba:a−b1
=\dfrac{\sqrt{a} \cdot \sqrt{a} \cdot \sqrt{b}+\sqrt{b} \cdot \sqrt{b} \cdot \sqrt{a}}{\sqrt{a b}}: \dfrac{1}{\sqrt{a}-\sqrt{b}}=aba⋅a⋅b+b⋅b⋅a:a−b1
=\dfrac{\sqrt{a} \cdot \sqrt{a b}+\sqrt{b} \cdot \sqrt{a b}}{\sqrt{a b}}: \dfrac{1}{\sqrt{a}-\sqrt{b}}=aba⋅ab+b⋅ab:a−b1
=\dfrac{\sqrt{a b}(\sqrt{a}+\sqrt{b})}{\sqrt{a b}} \cdot(\sqrt{a}-\sqrt{b})=abab(a+b)⋅(a−b)
=(\sqrt{a}+\sqrt{b}) \cdot(\sqrt{a}-\sqrt{b})=(a+b)⋅(a−b)
=a-b=V P=a−b=VP.
d) VT=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)VT=(1+a+1a+a)(1−a−1a−a)
=\left(1+\dfrac{\sqrt{a} \cdot \sqrt{a}+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a} \cdot \sqrt{a}-\sqrt{a}}{\sqrt{a}-1}\right)=(1+a+1a⋅a+a)(1−a−1a⋅a−a)
=\left[1+\dfrac{\sqrt{a}(\sqrt{a}+1)}{\sqrt{a}+1}\right]\left[1-\dfrac{\sqrt{a}(\sqrt{a}-1)}{\sqrt{a}-1}\right]=[1+a+1a(a+1)][1−a−1a(a−1)]
=(1+\sqrt{a})(1-\sqrt{a})=(1+a)(1−a)
=1-(\sqrt{a})^{2}=1-a=V P=1−(a)2=1−a=VP

a: \(=\sqrt{5}+2+\sqrt{3}+1-\sqrt{5}-\sqrt{3}=3\)
b: \(=\left(-\sqrt{5}-2+\sqrt{5}-\sqrt{3}\right)\cdot\left(2\sqrt{3}+3\right)\)
\(=-\sqrt{3}\left(2+\sqrt{3}\right)\cdot\left(2+\sqrt{3}\right)\)
\(=-\sqrt{3}\left(7+4\sqrt{3}\right)=-7\sqrt{3}-12\)
c: \(=\dfrac{\sqrt{2}+\sqrt{3}+2}{\left(\sqrt{2}+\sqrt{3}+2\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+2\right)}=\dfrac{1}{1+\sqrt{2}}=\sqrt{2}-1\)

Bài 2:
\(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2.\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(P=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2.\left(\dfrac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(P=\left[\dfrac{\left(a-1\right)^2}{4a}\right].\left(\dfrac{\left(\sqrt{a}-1+\sqrt{a}+1\right)\left(\sqrt{a}-1\right)-\sqrt{a}-1}{a-1}\right)\)
\(P=\dfrac{\left(a-1\right)^2}{4a}.\dfrac{2\sqrt{a}.\left(-2\right)}{a-1}\)
\(P=\dfrac{\left(a-1\right)^2\left(-4\sqrt{a}\right)}{4a.\left(a-1\right)}\)
\(P=\dfrac{\left(a-1\right).\left(-\sqrt{a}\right)}{a}=\dfrac{-a\sqrt{a}+\sqrt{a}}{a}\)
Bài 1:
\(A=\dfrac{2}{\sqrt{2}}-\dfrac{1}{\sqrt{3}-\sqrt{2}}+\dfrac{2}{\sqrt{3}-1}\)\(A=\dfrac{2\sqrt{2}}{2}-\dfrac{1\left(\sqrt{3}+\sqrt{2}\right)}{3-2}+\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}\right)^2-1}\)
\(A=\sqrt{2}-\dfrac{\sqrt{3}+\sqrt{2}}{1}+\dfrac{2\left(\sqrt{3}+1\right)}{3-1}\)
\(A=\sqrt{2}-\sqrt{3}-\sqrt{2}+\sqrt{3}+1\)
\(A=1\)

a:
Sửa đề: \(\left(\dfrac{7-\sqrt{7}}{\sqrt{7}}-2\right)\left(\dfrac{6}{\sqrt{7}+1}+4\right)\)
\(=\left(\sqrt{7}-1-2\right)\left(\sqrt{7}-1+4\right)\)
\(=\left(\sqrt{7}-3\right)\left(\sqrt{7}+3\right)=7-9=-2\)
b: \(=\sqrt{\dfrac{5-2\sqrt{6}}{12}}+\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}}{2\sqrt{3}}+\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}+\sqrt{2}}{2\sqrt{3}}=\dfrac{1}{2}\)

\(a.\dfrac{\sqrt{7}-5}{2}-\dfrac{6}{\sqrt{7}-2}+\dfrac{1}{3+\sqrt{7}}+\dfrac{3}{5+2\sqrt{7}}=\dfrac{\sqrt{7}-5}{2}+\dfrac{3-\sqrt{7}}{2}+\dfrac{6\sqrt{7}-15}{3}-\dfrac{6\sqrt{7}+12}{3}=-10\)
\(b.\left(\sqrt{10}+\sqrt{2}\right)\left(6-2\sqrt{5}\right)\sqrt{3+\sqrt{5}}=\left(\sqrt{5}+1\right)\left(6-2\sqrt{5}\right)\sqrt{5+2\sqrt{5}+1}=\left(\sqrt{5}+1\right)^2\left(6-2\sqrt{5}\right)=\left(6+2\sqrt{5}\right)\left(6-2\sqrt{5}\right)=36-20=16\)

\(A=\sqrt{8}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =2\sqrt{2}-\sqrt{7}+5\sqrt{7}+2\sqrt{2}\\ =4\sqrt{2}+4\sqrt{7}\)
\(B=\left(3+2\sqrt{6}+2\right)\left(25-20\sqrt{6}+24\right)\sqrt{3-2\sqrt{6}+2}\\ =\left(\sqrt{3}+\sqrt{2}\right)^2\left(5-2\sqrt{6}\right)^2\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}+\sqrt{2}\right)\left(3-2\sqrt{6}+2\right)^2\\ =\left(\sqrt{3}-\sqrt{2}\right)^3\\ =9\sqrt{3}-11\sqrt{2}\)

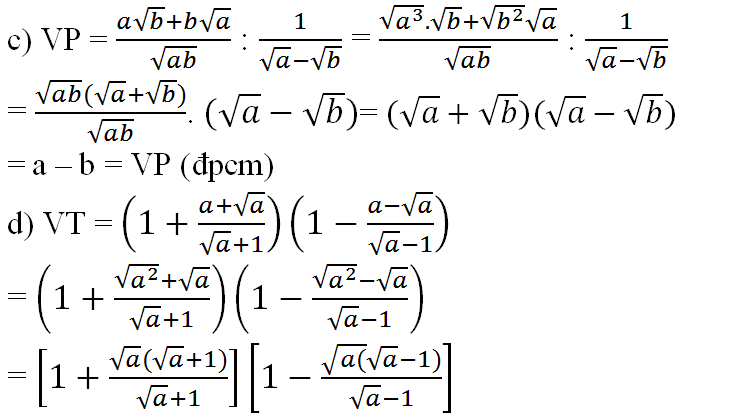
ĐKXĐ: a>=6
\(\dfrac{a-7}{\sqrt{a-6}+1}=\sqrt{a-6}-1\)
\(A=\dfrac{\left|a-5\right|}{5-a}+\sqrt{a-6}\)
\(=\dfrac{a-5}{5-a}+\sqrt{a-6}=\sqrt{a-6}-1\)(ĐPCM)