Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

N = \(\dfrac{1}{10^2}+\dfrac{1}{11^2}+\dfrac{1}{12^2}+...+\dfrac{1}{n^2}\)
= \(\dfrac{1}{10.10}+\dfrac{1}{11.11}+\dfrac{1}{12.12}+...+\dfrac{1}{n.n}\)
=> N < \(\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}+...+\dfrac{1}{\left(n-1\right).n}\)
=> N < \(\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(=>N< \dfrac{1}{9}-\dfrac{1}{n}\)
=> N < \(\dfrac{1}{9}\)
Vậy N < \(\dfrac{1}{9}\)

\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{\left(n-1\right)n}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(=1-\dfrac{1}{n}< 1\)
\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1\left(đpcm\right)\)

\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{n\left(n+3\right)}\)
\(\Rightarrow S=\dfrac{4-1}{1.4}+\dfrac{7-4}{4.7}+\dfrac{10-7}{7.10}+...+\dfrac{\left(n+3\right)-n}{n\left(n+3\right)}\)
\(\Rightarrow S=\dfrac{4}{1.4}-\dfrac{1}{1.4}+\dfrac{7}{4.7}-\dfrac{4}{4.7}+\dfrac{10}{7.10}-\dfrac{7}{7.10}+...+\dfrac{n+3}{n\left(n+3\right)}-\dfrac{n}{n\left(n+3\right)}\)
\(\Rightarrow S=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{n}-\dfrac{1}{n+3}\)
\(\Rightarrow S=1-\dfrac{1}{n+3}< 1\Rightarrow S< 1\)
Vậy S < 1

Bài 3:
Để A là số nguyên thì \(n-2+5⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{3;1;7;-3\right\}\)

a, Ta có :
\(M=\dfrac{1}{1\cdot2}+\dfrac{1}{1\cdot2\cdot3}+\dfrac{1}{1\cdot2\cdot3\cdot4}+...+\dfrac{1}{1\cdot2\cdot3\cdot...\cdot100}\\ < \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-...+\dfrac{1}{99}-\dfrac{1}{100}\\ =1-\dfrac{1}{100}=\dfrac{99}{100}< 1\\ \Rightarrow M< 1\\ \RightarrowĐpcm\)

\(A=\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+...+\dfrac{1}{8}.\dfrac{1}{9}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{9}\)
\(=\dfrac{7}{18}\)
\(B=\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{110}\)
\(=\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{10.11}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(=\dfrac{1}{4}-\dfrac{1}{11}\)
\(=\dfrac{7}{44}\)

a) Để A là phân số thì 5 không chia hết cho n-1 hay n-1 không phải Ư(5) mà Ư(5)={-5;-1;1;5}
Ta có bảng sau:
| \(n-1\ne\) | -5 | -1 | 1 | 5 |
| \(n\ne\) | -4 | 0 | 2 | 6 |
Vậy n\(\ne\left\{-4;0;2;6\right\}\)thì A là phân số
n=0 => A=\(\dfrac{5}{0-1}=-5\)
n=10 => A=\(\dfrac{5}{10-1}=\dfrac{5}{9}\)
n=-2 => A=\(\dfrac{5}{-2-1}=-\dfrac{5}{3}\)
Để A là số nguyên =>5 chia hết cho n-1 <=>n-1 là Ư(5)
Từ bảng trên => n={-4;0;2;6} thì A nguyên
b) Do n là Số tự nhiên => n và n+1 là 2 số tự nhiên liên tiếp
=>n và n+1 nguyên tố cùng nhau
=>phân số \(\dfrac{n}{n+1}\)tối giản(dpcm)
c)\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{49\cdot50}=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}=1-\dfrac{1}{50}< 1\left(đpcm\right)\)
c) 1/1.2 + 1/2.3 + 1/3.4 + .....+ 1/49.50
= 1/1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5 + ......+ 1/49 - 1/50
tới bước đây mik làm gọn lại chút nha
= 1/1 - 1/50
=49/50
Suy ra : 49/50 <1 ( điều phải chứng minh )

a) M =1+3+32+33+......+3118+3119
M = ( 1+3+32 ) +...+ ( 3117 + 3118+3119 )
M = 1. ( 1+3+32 ) + ... + 3117 . ( 3117 + 3118+3119 )
M = ( 1+3+32 ) .( 1 + ... + 3117 )
M = 13 . ( 1 + ... + 3117 ) \(⋮\) 13 (đpcm )
b) Ta có:
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)
...
\(\dfrac{1}{2009^2}< \dfrac{1}{2008.2009}\)
\(\dfrac{1}{2010^2}< \dfrac{1}{2009.2010}\)
=> \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2009^2}+\dfrac{1}{2010^2}\) < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2008.2009}+\dfrac{1}{2009.2010}\) (1)
Biến đổi vế trái:
\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2008.2009}+\dfrac{1}{2009.2010}\)
= \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2008}-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2010}\)
= \(1-\dfrac{1}{2010}\)
= \(\dfrac{2009}{2010}< 1\) (2)
Từ (1) và (2), suy ra :
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2009^2}+\dfrac{1}{2010^2}\) < 1 hay:
N < 1
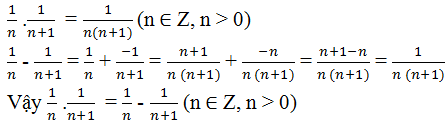

\(n^2>n^2-n=n\left(n-1\right)\Rightarrow\dfrac{1}{n^2}< \dfrac{1}{n\left(n-1\right)}\Rightarrow\dfrac{1}{n^2}< \dfrac{1}{n-1}-\dfrac{1}{n}\)