Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hiển nhiên nếu z
∈
R, z
≠
−1 thì 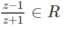
Ngược lại, nếu 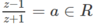
thì z – 1 = az + a và a ≠ 1
Suy ra (1 − a)z = a + 1
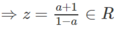
và hiển nhiên z ≠ −1.

Hiển nhiên nếu z ∈ R, z ≠ −1 thì 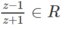
Ngược lại, nếu 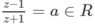
thì z – 1 = az + a và a ≠ 1
Suy ra (1 − a)z = a + 1
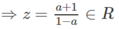
và hiển nhiên z ≠ −1.

\(a^2=\left|z+\frac{1}{z}\right|^2=\left(z+\frac{1}{z}\right)\left(\overline{z}+\frac{1}{z}\right)=\left|z\right|^2+\frac{z^2+\overline{z}^2}{\left|z\right|^2}+\frac{1}{\left|z\right|^2}\)
\(=\frac{\left|z\right|^4+\left(z+\overline{z}\right)^2-2\left|z\right|^2+1}{\left|z\right|^2}\)
Do đó :
\(\left|z\right|^4-\left|z\right|^2\left(a^2+2\right)+1=-\left(z+\overline{z}\right)^2\le0\)
\(\Rightarrow\left|z\right|^2\in\left[\frac{a^2+2-\sqrt{a^4+4a^2}}{2};\frac{a^2+2+\sqrt{a^4+4a^2}}{2}\right]\)
\(\Rightarrow\left|z\right|\in\left[\frac{-a+\sqrt{a^4+4a^2}}{2};\frac{a+\sqrt{a^4+4a^2}}{2}\right]\)
max \(\left|z\right|=\frac{a+\sqrt{a^4+4a^2}}{2}\)
min \(\left|z\right|=;\frac{a+\sqrt{a^4+4a^2}}{2}\)
\(\Leftrightarrow z\in M,z=-\overline{z}\)

Giả sử z = a + bi
Khi đó: |z|=√a2+b2|z|=a2+b2
Từ đó suy ra:
|z|=√a2=|a|≥a,|z|=√b2=|b|≥b
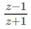
Hiển nhiên nếu \(z\in\mathbb{R},z\ne-1\) thì \(\dfrac{z-1}{z+1}\in\mathbb{R}\)
Ngược lại, nếu \(\dfrac{z-1}{z+1}=a\in\mathbb{R}\) thì \(z-1=az+a\) và \(a\ne1\)
Suy ra \(\left(1-a\right)z=a+1\Rightarrow\)\(z=\dfrac{a+1}{1-a}\in\mathbb{R}\) và hiển nhiên \(z\ne-1\)