
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có với n=1: VT=1=VP
giả sử đúng với n=k, k thuộc N*
ta cần chứng minh đúng với n=k+1
thay vào ta dduocj: [k(k+1)]2/4+(k+1)3=[(k+1)(k+2)]^2/4
=> đpcm
phương pháp quy nạp


- Với \(n=4\Rightarrow3^3>4.6\) (đúng)
- Giả sử BĐT đã cho đúng với \(n=k\ge4\) hay \(3^{k-1}>k\left(k+2\right)\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay: \(3^k>\left(k+1\right)\left(k+3\right)\)
Thật vậy, do \(k\ge4\Rightarrow k-3>0\), ta có:
\(3^k=3.3^{k-1}>3k\left(k+2\right)=3k^2+6k=\left(k^2+4k+3\right)+\left(2k^2+2k-3\right)\)
\(=\left(k+1\right)\left(k+3\right)+2k^2+k+\left(k-3\right)>\left(k+1\right)\left(k+3\right)\) (đpcm)

Dễ thấy dấu"=" xảy ra khi x=1
Giả sử bđt đúng với n=k>1 tức là
\(3^k\ge2k+1\) (1)
Nhân cả 2 vế của (1) với 3 ta được
\(3^{k+1}\ge6k+3\Leftrightarrow3^{k+1}\ge3k+4+3k-1\)
Vì 3k-1>0
=>\(3^{k+1}\ge3\left(k+1\right)+1\)
Vậy bđt đúng với n=k+1
=> bđt được chứng minh


\(\left(1+\dfrac{1}{n}\right)^n=C_n^0+C_n^1.\dfrac{1}{n}+C_n^2.\dfrac{1}{n^2}+...+C_n^n.\dfrac{1}{n^n}\)
\(=1+1+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}\)
\(=2+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}>2\)
Mặt khác:
\(C_n^k.\dfrac{1}{n^k}=\dfrac{n!}{k!\left(n-k\right)!.n^k}=\dfrac{\left(n-k+1\right)\left(n-k+2\right)...n}{n^k}.\dfrac{1}{k!}< \dfrac{n.n...n}{n^k}.\dfrac{1}{k!}=\dfrac{n^k}{n^k}.\dfrac{1}{k!}=\dfrac{1}{k!}\)
\(< \dfrac{1}{k\left(k-1\right)}=\dfrac{1}{k-1}-\dfrac{1}{k}\)
Do đó:
\(C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}=1-\dfrac{1}{n}< 1\)
\(\Rightarrow2+C_n^2.\dfrac{1}{n^2}+C_n^3.\dfrac{1}{n^3}+...+C_n^n.\dfrac{1}{n^n}< 2+1=3\) (đpcm)
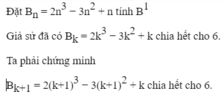

a.
Với \(n=1\Rightarrow4\ge3+1\) (đúng)
Giả sử đẳng thức đúng với \(n=k\ge1\) hay \(4^k\ge3k+1\)
Ta cần chứng minh nó cũng đúng với n=k+1 hay: \(4^{k+1}\ge3\left(k+1\right)+1\)
Thật vậy, ta có:
\(4^{k+1}=4.4^k\ge4\left(3k+1\right)=12k+4=3\left(k+1\right)+1+9k>3\left(k+1\right)+1\) (đpcm)
b.
Với \(n=1\Rightarrow\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}>1\) (đúng)
Giả sử BĐT đúng với \(n=k\) hay: \(\dfrac{1}{k+1}+\dfrac{1}{k+2}+...+\dfrac{1}{3k+1}>1\)
\(\Rightarrow\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3k+1}>1-\dfrac{1}{k+1}\)
Ta cần chứng minh nó cũng đúng với n=k+1 hay:
\(\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3\left(k+1\right)+1}>1\)
\(\Leftrightarrow\dfrac{1}{k+2}+\dfrac{1}{k+3}+...+\dfrac{1}{3k+4}>1\)
Thật vạy, ta có:
\(\dfrac{1}{k+2}+\dfrac{1}{k+3}+..+\dfrac{1}{3k+4}\)
\(=\dfrac{1}{k+2}+...+\dfrac{1}{3k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}\)
\(>1-\dfrac{1}{k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}\) (1)
Mặt khác ta có:
\(\dfrac{1}{3k+2}+\dfrac{1}{3k+4}-\dfrac{2}{3k+3}=\dfrac{2}{\left(3k+2\right)\left(3k+3\right)\left(3k+4\right)}>0\)
\(\Rightarrow\dfrac{1}{3k+2}+\dfrac{1}{3k+4}>\dfrac{2}{3k+3}\)
\(\Rightarrow\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}>\dfrac{3}{3k+3}=\dfrac{1}{k+1}\) (2)
(1);(2) \(\Rightarrow1-\dfrac{1}{k+1}+\dfrac{1}{3k+2}+\dfrac{1}{3k+3}+\dfrac{1}{3k+4}>1\) (đpcm)