Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(A=\frac{1}{2}+\frac{1}{33}+\frac{1}{34}+\frac{1}{35}+\frac{1}{51}+\frac{1}{53}+\frac{1}{55}+\frac{1}{57}+\frac{1}{59}\)
Ta có:
\(\frac{1}{33}+\frac{1}{34}+\frac{1}{35}< \frac{1}{30}+\frac{1}{30}+\frac{1}{30}=\frac{3}{30}=\frac{1}{10}\)
\(\frac{1}{51}+\frac{1}{53}+\frac{1}{55}+\frac{1}{57}+\frac{1}{59}< \frac{1}{50}+\frac{1}{50}+\frac{1}{50}+\frac{1}{50}+\frac{1}{50}=\frac{5}{50}=\frac{1}{10}\)
Cộng theo vế:
\(\frac{1}{33}+\frac{1}{34}+\frac{1}{35}+\frac{1}{51}+\frac{1}{53}+\frac{1}{55}+\frac{1}{57}+\frac{1}{59}< \frac{2}{10}=\frac{1}{5}\)
Suy ra \(A< \frac{1}{2}+\frac{1}{5}=\frac{7}{10}\)
Ta có đpcm.

a: \(=\dfrac{-12}{7}\left(\dfrac{4}{35}+\dfrac{31}{35}\right)-\dfrac{2}{7}=\dfrac{-12}{7}-\dfrac{2}{7}=-2\)
b: =(-4)+(-4)+...+(-4)
=-4*25=-100
c: \(=157\cdot\left(-37\right)-41\cdot53+37\cdot157+51\cdot53\)
=10*53
=530

Ta có :
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(S=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét :
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{2}\rightarrowđpcm\)

1: \(=\dfrac{15}{37}\cdot\dfrac{38}{41}-\dfrac{15}{37}\cdot\dfrac{74}{45}-\dfrac{38}{41}\cdot\dfrac{15}{37}-\dfrac{38}{41}\cdot\dfrac{82}{76}\)
\(=\dfrac{-2}{3}-1=-\dfrac{5}{3}\)
2: \(=\dfrac{47}{53}\cdot\dfrac{17}{3}-\dfrac{47}{53}\cdot\dfrac{53}{47}+\dfrac{17}{3}\cdot\dfrac{6}{17}-\dfrac{17}{3}\cdot\dfrac{47}{53}\)
\(=-1+2=1\)

Ta thấy:
\(\dfrac{1}{51}< \dfrac{1}{50}\)
\(\dfrac{1}{52}< \dfrac{1}{50}\)
...
\(\dfrac{1}{100}< \dfrac{1}{50}\)
\(\Rightarrow\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}< \dfrac{1}{50}.50=1\)
\(\Rightarrow\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}< 1\left(1\right)\)
Lại có:
\(\dfrac{1}{51}>\dfrac{1}{100}\)
\(\dfrac{1}{52}>\dfrac{1}{100}\)
...
\(\dfrac{1}{100}=\dfrac{1}{100}\)
\(\Rightarrow\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}>\dfrac{1}{100}.50=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}>\dfrac{1}{2}\left(2\right)\)
Từ (1),(2)\(\Rightarrow\)\(\dfrac{1}{2}< \dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}< 1\)

Giải:
Ta có: \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)\) \(+\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Dễ thấy:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S< \dfrac{1}{2}\) (Đpcm)

Sai đề. Sửa đề :v
Cmr: \(\dfrac{1}{5}+\dfrac{1}{14}+\dfrac{1}{28}+\dfrac{1}{44}+\dfrac{1}{61}+\dfrac{1}{85}+\dfrac{1}{97}< \dfrac{1}{2}\)
Giải:
Đặt \(A=\dfrac{1}{5}+\dfrac{1}{14}+\dfrac{1}{28}+\dfrac{1}{44}+\dfrac{1}{61}+\dfrac{1}{85}+\dfrac{1}{97}\)
Ta có:
\(A=\dfrac{1}{5}+\left(\dfrac{1}{14}+\dfrac{1}{28}+\dfrac{1}{44}\right)+\left(\dfrac{1}{61}+\dfrac{1}{85}+\dfrac{1}{97}\right)\)
\(A< \dfrac{1}{5}\left(\dfrac{1}{14.3}\right)+\left(\dfrac{1}{61.3}\right)\)
\(A< \dfrac{1}{5}+\dfrac{3}{14}+\dfrac{3}{61}\)
\(A< \dfrac{1}{5}+\dfrac{3}{12}+\dfrac{1}{20}\)
\(A< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}\)
\(\Rightarrow A< \dfrac{1}{2}\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{14}+\dfrac{1}{28}+\dfrac{1}{44}+\dfrac{1}{61}+\dfrac{1}{85}+\dfrac{1}{97}< \dfrac{1}{2}\) \((đpcm)\)
I'm don't knowwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwwww!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!![]()

\(-1\dfrac{1}{5}.\dfrac{12+\dfrac{4}{3}-\dfrac{12}{37}-\dfrac{12}{35}}{3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}}:\dfrac{4+\dfrac{4}{17}+\dfrac{4}{19}+\dfrac{4}{2003}}{5+\dfrac{5}{17}+\dfrac{5}{19}+\dfrac{5}{2003}}\)
\(=\dfrac{-6}{5}.\dfrac{4\left(3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}\right)}{3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{35}}:\dfrac{4\left(1+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{2003}\right)}{5\left(1+\dfrac{1}{17}+\dfrac{1}{19}+\dfrac{1}{2003}\right)}\)
\(=\dfrac{-6}{5}.4:\dfrac{4}{5}\)
\(=\dfrac{-6.4.5}{5.4}=-6\)

Giải:
Ta có:
\(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\)
\(=\dfrac{1}{5}+\left(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}\right)+\) \(\left(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\right)\)
Nhận xét:
\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}< \dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{4}\)
\(\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow S< \dfrac{1}{5}+\dfrac{1}{4}+\dfrac{1}{20}=\dfrac{1}{2}\)
Vậy \(S=\dfrac{1}{5}+\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{61}+\dfrac{1}{62}+\dfrac{1}{63}\) \(< \dfrac{1}{2}\) (Đpcm)
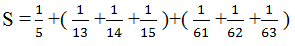
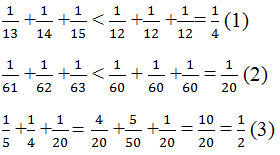
Đặt \(A=\frac{1}{3}+\frac{1}{31}+\frac{1}{35}+\frac{1}{37}+\frac{1}{47}+\frac{1}{53}+\frac{1}{61}\)
Ta có:
\(A=\frac{1}{3}+\frac{1}{31}+\frac{1}{35}+\frac{1}{37}+\frac{1}{47}+\frac{1}{53}+\frac{1}{61}\)
\(\Rightarrow A=\frac{1}{3}+\left(\frac{1}{31}+\frac{1}{35}+\frac{1}{37}\right)+\left(\frac{1}{47}+\frac{1}{53}+\frac{1}{61}\right)\)
Nhận xét:
\(\frac{1}{31}+\frac{1}{35}+\frac{1}{37}< \frac{1}{30}+\frac{1}{30}+\frac{1}{30}\)
\(\frac{1}{47}+\frac{1}{53}+\frac{1}{61}< \frac{1}{45}+\frac{1}{45}+\frac{1}{45}\)
\(\Rightarrow A< \frac{1}{3}+\left(\frac{1}{30}+\frac{1}{30}+\frac{1}{30}\right)+\left(\frac{1}{45}+\frac{1}{45}+\frac{1}{45}\right)\)
Mà \(\frac{1}{3}+\left(\frac{1}{30}+\frac{1}{30}+\frac{1}{30}\right)+\left(\frac{1}{45}+\frac{1}{45}+\frac{1}{45}\right)=\frac{1}{3}+\frac{1}{10}+\frac{1}{15}=\frac{1}{2}\)
\(\Rightarrow A< \frac{1}{2}\)
Vậy \(\frac{1}{3}+\frac{1}{31}+\frac{1}{35}+\frac{1}{37}+\frac{1}{47}+\frac{1}{53}+\frac{1}{61}< \frac{1}{2}\) (Đpcm)
tại sao bạn biết 1/30 va 1/45