Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 3 số đó là a - d, a, a + d rồi áp dụng tính chất của cấp số cộng và cấp số nhân.

Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389

Chọn C
*Theo tính chất của cấp số cộng , ta có x+ z = 2y.
Kết hợp với giả thiết, x+ y + z = 21, ta suy ra 3y = 21 nên y = 7.
* Gọi d là công sai của cấp số cộng thì x = y − d = 7 − d và z = y + d = 7 + d .
Sau khi thêm các số 2 ; 3 ; 9 vào ba số x ; y ; z ta được ba số là x+ 2 ; y + 3 ; z + 9 hay
9- d ; 10 ; 16+ d.
* Theo tính chất của cấp số nhân, ta có
9 − d 16 + d = 10 2 ⇔ d 2 + 7 d − 44 = 0
Giải phương trình ta được d= -11 hoặc d= 4.
Với d = -11 ; cấp số cộng 18 ; 7 ; - 4. Lúc này F = 389.
Với d= 4, cấp số cộng 3 ; 7 ; 11. Lúc này F = 179.

Gọi 3 số cần tìm lần lượt là: \({u_{n - 1}},\;{u_n},\;{u_{n + 1}}\)
Theo tính chất của cấp số cộng ta có: \({u_{n - 1}} + {u_{n + 1}} = 2{u_n}\)
Mà đề bài: \({u_{n - 1}} + {u_n} + {u_{n + 1}} = 21\) suy ra \(3{u_n} = 21\;\)
\(\begin{array}{l} \Leftrightarrow {u_n} = 7\\ \Leftrightarrow \left\{ \begin{array}{l}{u_{n - 1}} = {u_n} - d = 7 - d\\{u_{n + 1}} = {u_n} + d = 7 + d\end{array} \right.\end{array}\)
Lần lượt cộng thêm các số 2, 3, 9 vào 3 số ta được: \({u_{n - 1}} + 2,\;{u_n} + 3,\;{u_{n + 1}} + 9\) hay \(9 - d,\;10,\;16 + d\)
Theo tính chất của cấp số nhân ta có:
\(\begin{array}{l}\left( {9 - d} \right)\left( {16 + d} \right) = {10^2}\\ \Leftrightarrow {d^2} + 7d - 44 = 0\\ \Leftrightarrow \left[ \begin{array}{l}d = - 11\\d = 4\end{array} \right.\end{array}\)
Vậy 3 số cần tìm là: 18; 7; -4 hoặc 3; 7; 11.

Ba số x, y, z lập thành một cấp số nhân nên:
y = x.q và z = y.q = x.q2 ( q là công bội)
Ba số x, 2y, 3z lậo thành một cấp số cộng nên:
x + 3z = 4y ⇔ x + 3.(xq2) = 4.(x.q)
⇔ x. (1 + 3q2 – 4q) = 0 ⇔ x = 0 hay 3q2 – 4q + 1 = 0
Nếu x = 0 thì x = y= z= 0, q là một số tùy ý
Nếu x ≠ 0 thì 3q2– 4q + 1 = 0 ⇔\(\Leftrightarrow\left[{}\begin{matrix}q=1\\q=\dfrac{1}{3}\end{matrix}\right.\).
Công bội của cấp số nhân là \(q=1\) hoặc \(q=\dfrac{1}{3}\).

Gọi công bội của CSN x ; y ; z là q.
⇒ y = x.q ; z = x.q2.
Lại có : x ; 2y ; 3z lập thành CSC
⇔ 2y – x = 3z – 2y
⇔ 2.xq – x = 3.xq2 – 2.xq
⇔ x(2q – 1) = x.(3q2 – 2q)
⇔ x.(3q2 – 4q + 1) = 0
+ Nếu x = 0 ⇒ y = z = 0
⇒ q không xác định.
+ Nếu x ≠ 0 ⇒ 3q2 – 4q + 1 = 0 ⇔ q = 1 hoặc 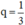
Vậy CSN có công bội q = 1 hoặc 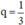

Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
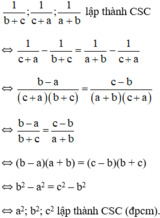
Gọi ba số đó là \(a,b,c\) theo ba số phải tìm. Theo bài ra ta có:
\(\left\{{}\begin{matrix}\dfrac{a+b}{2}=c\\ab=c^2\end{matrix}\right.\)\(\Rightarrow\left(\dfrac{a+b}{2}\right)^2=ab\)\(\Leftrightarrow a^2+b^2=2ab\)\(\Leftrightarrow\left(a-b\right)^2=0\)\(\Leftrightarrow a-b=0\)\(\Leftrightarrow a=b\).
Suy ra: \(c=\dfrac{a+b}{2}=\dfrac{a+a}{2}=a\).
Vì vậy: \(a=b=c\).