Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

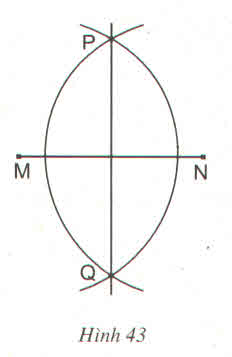
Ta có : Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
⇒ P; Q cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.

Hướng dẫn:

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

Hướng dẫn:
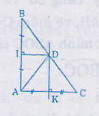
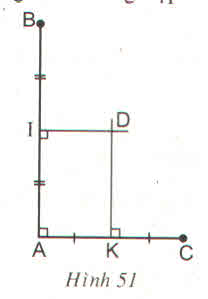
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800

Hướng dẫn :
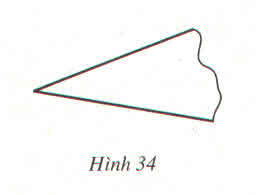
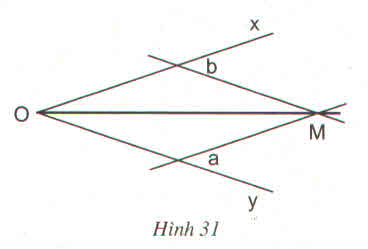
Theo cách vẽ thì M cách đều hai cạnh Ox, Oy (cùng bằng khoảng cách 2 lề của chiếc thước
Vì M cách đều Ox, Oy nên theo định lí đảo M thuộc phân giác của ˆxOyxOy^ hay OM là phân giác của ˆ

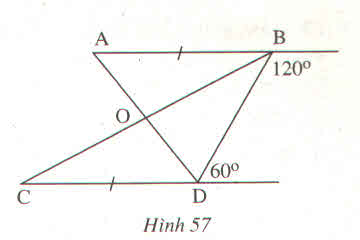
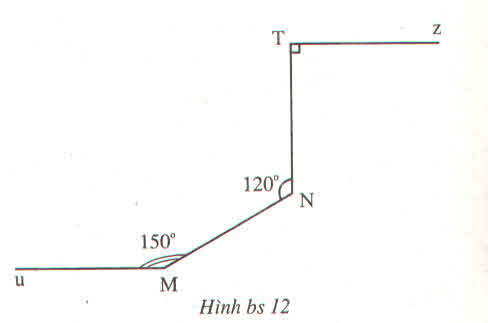
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC

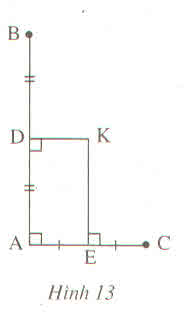
B D A E C K 1 2 3 4
Nối KA,KB,KC.
Ta có KD là đường trung trực AB
=>KA=KB(tính chất đường trung trực)
\(\Rightarrow\Delta KAB\) cân tại K nên KD là đường phân giác của \(\widehat{AKB}\)
\(\Rightarrow\widehat{K_1}=\widehat{K_3}\)
\(\Rightarrow\widehat{AKB}=2\widehat{K_1}\) (1)
KE là đường trung trực của AC
=>KA=KC(tính chất đường trung trực)
\(\Rightarrow\Delta KAC\) cân tại K nên KE là đường phân giác của \(\widehat{AKC}\)
\(\Rightarrow\widehat{K_2}=\widehat{K_4}\)
\(\Rightarrow\widehat{AKC}=2\widehat{K_2}\left(2\right)\)
\(KD\perp AB\left(gt\right)\)
\(AC\perp AB\left(gt\right)\)

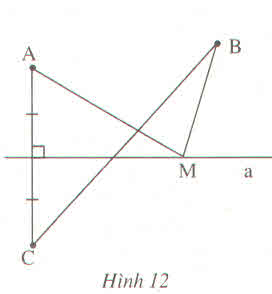
a: Gọi N là giao điểm của BC với a
Nếu M khác N
Vì M nằm trên đường trung trực của AC
nên MA=MC
XétΔMBC có BC<MB+MC
=>BC<MA+MB
Nếu M trùng với N thì nối NA
Vì N nằm trên đường trung trực của AC nên NA=NC
=>MA+MB=NA+NB=BC
=>MA+MB>=BC
b: MA+MB nhỏ nhất khi M là giao điểm của BC với a




Hướng dẫn:
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Hướng dẫn:
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN