Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho d'∥d, d"∥d, a\(⊥\)d
a d" d' d
- d' ∥ d (gt)
a\(⊥\)d (gt)
\(\Rightarrow\) a\(⊥\)d' (từ vuông góc đến song song) (1) - d" ∥ d (gt)
a\(⊥\)d (gt)
\(\Rightarrow\) a\(⊥\)d" (từ vuông góc đến song song) (2) - Từ (1) và (2) \(\Rightarrow\)d' ∥ d" (từ vuông góc đến song song)
d' ∥ d (gt), d" ∥ d (gt)
\(\Rightarrow\)d ∥ d' ∥ d"

ta có a, b, c là 3 đường thẳng phân biệt và a//b, c//b
giả sử a cắt c tại O
như vậy qua O ta kẻ được hai đường thẳng a và c cùng // với c như vậy trái với tiên đề Oclit (qua 1 điểm nằm ngoài đường thẳng ta chỉ kẻ được 1 và chỉ 1 đường thẳng // vơi đường thẳng đã cho)
=> a //c

Hỏi nhiều quá , mà thà bạn nói ko cần vẽ hình thì còn giải , đằng này đã vẽ hình còn phải ghi GT , KL . mệt !!!!!!!!!!! @_@
Chứng Minh Định lý hai đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau

d:
Giả thiết: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
Kết luận: \(\widehat{xAy}=\widehat{x'Ay'}\)

Ta có :
Giả thiết : Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba
Kết luận : chúng song song với nhau

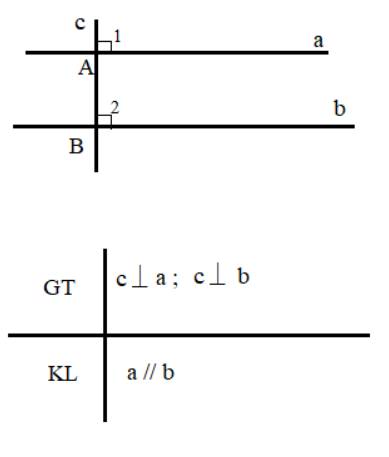
GT:Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
KL:Chúng song song với nhau.
Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
Kết luận: chúng song song với nhau
Chứng minh định lí hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song