Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

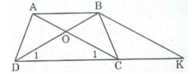
Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.
Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK
Mà AC = BD (gt)
Suy ra: BD = BK do đó ∆ BDK cân tại B
⇒ ∠ D 1 = ∠ K (tính chất hai tam giác cân)
Ta lại có: ∠ C 1 = ∠ K (hai góc đồng vị)
Suy ra: ∠ D 1 = ∠ C 1
Xét ∆ ACD và ∆ BDC:
AC = BD (gt)
∠ C 1 = ∠ D 1 (chứng minh trên)
CD chung
Do đó ∆ ACD = ∆ BDC (c.g.c) ⇒ ∠ (ADC) = ∠ (BCD)
Hình thang ABCD có ∠ (ADC) = ∠ (BCD) nên là hình thang cân.

c/m bai` nay` như sau:goi hi`nh thang la ABCD,qua B kẻ đuong thẳng //với AC cắt DC tại E
a)đâu tiên em chứng minh tam giac BDE la tam giac cân tại B:ta co ACD=BAC(AB//CD)
ma` ACD =BEC =>BEC=BAC
xet tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
ma `BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hi`nh thang cân (dfcm)
Chuc bạn học tốt!!!!

A B C D E 1 1
Kẻ BE // AC (\(E \in DC\))
Hình thang ABEC (AB // CE) có 2 cạnh bên BE // AC.
=> BE = AC.
Mà AC = BD.
=> BE = BD.
=> ΔBDE cân tại B.
=> \(\widehat{D_1}=\widehat{E}\) (1)
Ta có: BE // AC (cách vẽ)
=> \(\widehat{C_1}=\widehat{E}\) (đồng vị)
Từ (1) và (2) suy ra \(\widehat{D_1}=\widehat{C_1}\)
Xét ΔADC và ΔBCD có:
+ AC = BD (gt)
+ \(\widehat{D_1}=\widehat{C_1}\) (cmt)
+ DC là cạnh chung.
=> ΔADC = ΔBCD (c - g - c)
=> \(\widehat{ADC}=\widehat{BCD}\) (2 góc tương ứng)
Suy ra: ABCD là hình thang cân (đpcm)

Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E.
Ta có:
Góc ACD = góc BED (tính chất góc hình bình hành)
mà gócBDE = gócBED ( BDE là tam giac cân tại B)
=> góc ACD= góc BDC
xét 2 tam giác ACD và tam giác BDC có:
+ AC = BD ( gt)
+ góc ACD = góc BDC
+có cùng cạnh CD
=> tam giác ACD = tam giác BDC ( cạnh,góc,cạnh)
xét hình thang ABCD:
AD = BC vì tam giác ACD = tam giác BDC
=> ABCD là hình thang cân.
Vậy hình thang có hai đường chéo bằng nhau là hình thang cân.(đpcm)

A B C D E 1 1
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\) cân
b ) Ta có : AC // BE
\(\Rightarrow\widehat{C}_1=\widehat{E}\) ( 3 )
Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\) ( 4 )
Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)
Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)
CD là cạnh chung
Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)
c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chúc bạn học tốt !!!
1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng:
a) BDEBDE là tam giác cân.
b) △ACD=△BDC.△ACD=△BDC.
c) Hình thang ABCDABCD là hình thang cân.
chúc hok tốt , k nha! sai cũng k

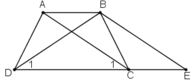
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Giả sử hình thang là ABCD,
Qua B kẻ đường thẳng với AC cắt DC tại E
a)Ta có ACD=BAC (AB//CD)
mà ACD =BEC =>BEC=BAC
Xét tam giac ABC va tam giác ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
mà BEC=ACD(đồng vị)=>ACD=BDC
xét tam giac ACD va tam giac BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tam giac ACD=tam giác BDC
=>ADC=BCD
=>ABCD la hình thang cân (dfcm)

Câu 1: trang 73 sách giáo khoa 8 tập 1
Câu 2: trang 73 sách giáo khoa 8 tập 1
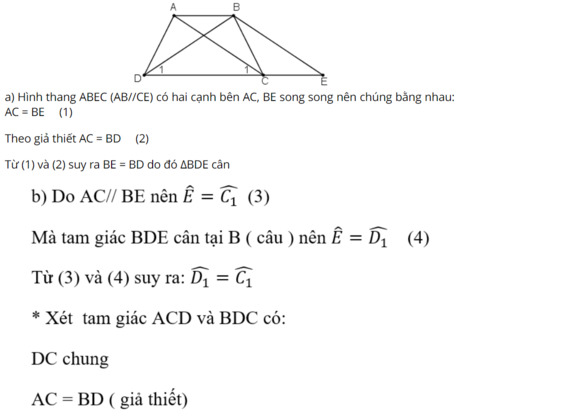


\(\) Xét hình thang ABCD (AB // CD) có AC = BD
Kẻ đường cao AH và BK => góc AHK = góc BKH = 90°
Do góc AHK = 90° mà AB // CD => BAH = 90°
=> góc BAH = góc AHK = góc HKB = 90°
=> Tứ giác ABKH là hình chữ nhật
=> AH = BK
Xét 2 tam giác vuông AHC và BKD :
AH = BK (cmt)
AC = BD (gt)
=> Tam giác AHC = Tam giác BKD (cạnh huyền - cgv)
=> góc ACD = góc BDC
Xét tam giác ACD và BDC :
AC = BD (gt)
góc ACD = góc BDC (cmt)
CD chung
=> Tam giác ACD = Tam giác BDC (c-g-c)
=> AD = BC
=> Hình thang ABCD có 2 cạnh bên bằng nhau : AD = BC