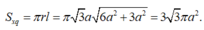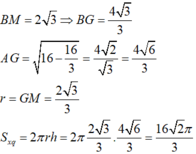Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)

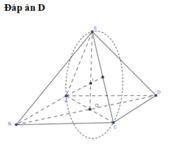
Kẻ SG vuông góc (ABC)
S.ABC là khối chóp đều
=>ΔABC đều
=>G là trọng tâm, là trực tâm của ΔABC
Gọi giao của AG với BC là D
=>D là trung điểm của BC
ΔABC đều có AD là trung tuyến
nên \(AD=\dfrac{a\sqrt{3}}{2}\)
=>\(AG=\dfrac{a\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{a\sqrt{3}}{3}\)
ΔSAG vuông tại G nên \(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{1}{3}a^2}\)
\(V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SG=\dfrac{1}{3}\cdot\sqrt{b^2-\dfrac{1}{3}a^2}\cdot\dfrac{a^2\sqrt{3}}{4}\)
\(=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{\dfrac{3b^2-a^2}{3}}\)
Thể tích khối tứ diện đều có cạnh bằng a là:
\(V=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a^3\sqrt{2}}{12}\)

a) Ta có: \({u_1} = 1,{u_2} = 2,{u_3} = 3\)
Dự đoán \({u_n} = n\)
b) Ta có: \(\begin{array}{l}{v_1} = 1\\{v_2} = 8 = {2^3}\\{v_3} = 27 = {3^3}\\{v_4} = 64 = {4^3}\end{array}\)
Dự đoán: \({v_n} = {n^3}\)

Đáp án A
Bán kính đáy của hình nón bằng bán kính ngoại tiếp đáy
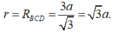
Chiều cao nón bằng chiều cao của tứ diện
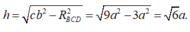
Vậy