NL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
2
TD
10 tháng 6 2021
Bn ko biết thì bn đừng nói, nói thế thừa lắm, ko ai hỏi bn đâu mà bn phải nói
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
a. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm2\pi\in D\)
Đồng thời:
\(y\left(x+2\pi\right)=sin\left(x+2\pi\right)+cos\left(2x+4\pi\right)=sinx+cos2x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=2\pi\)
b. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm\dfrac{2\pi}{3}\in D\)
\(y\left(x+\dfrac{2\pi}{3}\right)=sin\left(3x+2\pi\right)=sin3x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=\dfrac{2\pi}{3}\)
TV
2
27 tháng 10 2023
Hàm số y=3*sin2x tuần hoàn theo chu kì là:
\(T=\dfrac{2\Omega}{2}=\Omega\)
=>Chọn C
4 tháng 9 2020
1. T= \(\frac{\pi}{\left|a\right|}=\frac{\pi}{3}\)
2. \(T_1=\frac{2\pi}{2}=\pi\) ; \(T_2=\frac{2\pi}{\frac{1}{2}}=4\pi\)
=> \(T=BCNN\left(\pi;4\pi\right)=4\pi\)
3. \(\left[{}\begin{matrix}5x-45^o=30^o+k360^o\\5x-45^o=-30^o+k360^o\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=75^o+k360^o\\5x=15^o+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=15^o+k72^o\\x=3^0+k72^o\end{matrix}\right.\) \(\left(k\in Z\right)\)
Cho k=-1 thì x= -57 độ or x= -69 độ nên lấy x= -57 độ là no âm lớn nhất => Chọn C
4. Có pt hoành độ giao điểm của 2 đths : sinx = sin3x
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=\pi-x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\left(k\in Z\right)\)
trong \(\left(\frac{-\pi}{2};\frac{3\pi}{2}\right)\) với \(x=k\pi\Rightarrow k\in\left\{0;1\right\}\)
với \(x=\frac{\pi}{4}+\frac{k\pi}{4}\Rightarrow k\in\left\{-1;0;1;2\right\}\)
Vậy 2 đths cắt nhau tại 6 điểm trong \(\left(\frac{-\pi}{2};\frac{3\pi}{2}\right)\)
5. cot = \(\sqrt{3}\) \(\Leftrightarrow tanx=\frac{1}{\sqrt{3}}\Leftrightarrow x=\frac{\pi}{6}+k\pi\left(k\in Z\right)\)
x \(\in\left[0;2017\pi\right]\Rightarrow k\in\left\{0;1;2;....;2015;2016\right\}\)
Vậy ptrinh có 2017 nghiệm.
CHÚC BẠN HỌC TỐT..!!
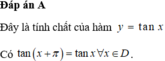
TXĐ: \(D=R\backslash\left\{\dfrac{\pi}{2}+k\pi\right\}\)
\(\forall x\in D\Rightarrow x+\pi\in D\) và \(x-\pi\in D\)
\(f\left(x+\pi\right)=tan\left(x+\pi\right)=tanx=f\left(x\right)\)
\(\Rightarrow\) Hàm y=tanx tuần hoàn với chu kì \(\pi\)