K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 1 2021
a) Xét (O) có
NA là tiếp tuyến có A là tiếp điểm(gt)
NE là tiếp tuyến có E là tiếp điểm(gt)
Do đó: ON là tia phân giác của \(\widehat{AOE}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{AOE}=2\cdot\widehat{EON}\)
Xét (O) có
ME là tiếp tuyến có E là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OM là tia phân giác của \(\widehat{EOB}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{EOB}=2\cdot\widehat{EOM}\)
Ta có: \(\widehat{EOA}+\widehat{EOB}=180^0\)(hai góc kề bù)
hay \(2\cdot\widehat{EON}+2\cdot\widehat{EOM}=180^0\)
\(\Leftrightarrow\widehat{EON}+\widehat{EOM}=90^0\)
hay \(\widehat{MON}=90^0\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào \(\Delta\)ONM vuông tại O có OE là đường cao ứng với cạnh huyền NM, ta được:
\(ME\cdot NE=OE^2\)
mà OE=R
nên \(ME\cdot NE=R^2\)(đpcm)
1 tháng 11 2021
a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MQ là tiếp tuyến có Q là tiếp điểm
Do đó: MA=MQ
Xét (O) có
EQ là tiếp tuyến có Q là tiếp điểm
EB là tiếp tuyến có B là tiếp điểm
Do đó: EQ=EB
Ta có: QM+QE=EM
hay EM=AM+BE
3 tháng 3 2022
a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
hay ΔCOD vuông tại O
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=MO^2=R^2=AC\cdot BD\)
PT
1
CM
27 tháng 10 2017
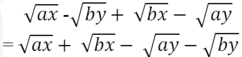
= √x(√a + √b) - √y(√a + √b)
= (√a + √b)(√x - √y) (với x, y, a và b đều không âm)