Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

để mình làm cho
\(P=\sin^6_a+\cos^6_a+3\sin_a^2+\cos^2_a=\left(\sin^2_a+\cos^2_a\right)\left(\sin^4_a-\sin^2_a\cos^2_a+\cos^4_a\right)\) \(+3.\sin^2_a.\cos^2_a\)
\(=\sin^4_a+2\sin^2_a.\cos^2_a+\cos^4_a=\left(\sin^2_a+\cos^2_a\right)^2=1\)
đề đoạn cuối phải là nhân chứ không phải +

Với x > 0; x ≠ 4; x ≠ 9 ta có:
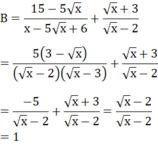
Vậy giá trị của B không phụ thuộc vào giá trị của biến x

\(\frac{2x}{x+3\sqrt{x}+2}+\frac{5\sqrt{x}+1}{x+4\sqrt{x}+3}+\frac{\sqrt{x}+10}{x+5\sqrt{x}+6}\)
\(=\frac{2x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}+\frac{5\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}+10}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\left(\sqrt{x}+3\right)+\left(5\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+\left(\sqrt{x}+10\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2\sqrt{x^3}+6x+5x+11\sqrt{x}+2+x+11\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{12x+22\sqrt{x}+2\sqrt{x^3}+12}{6x+11\sqrt{x}+\sqrt{x^3}+6}\)
\(=\frac{2\left(6x+11\sqrt{x}+\sqrt{x^3}+6\right)}{6x+11\sqrt{x}+\sqrt{x^3}+6}\)
\(=2\) (ko phụ thuộc vào biến ) (đpcm)

\(\left(\sqrt[3]{x}+1\right)^3-\left(\sqrt[3]{x}-1\right)^3-6\left(\sqrt[3]{x}-1\right)\left(\sqrt[3]{x}+1\right)\\ =x+3\sqrt[3]{x^2}+3\sqrt[3]{x}+1-\left(x-3\sqrt[3]{x^2}+3\sqrt[3]{x}-1\right)-6\left(\sqrt[3]{x^2}-1\right)\\ =x+3\sqrt[3]{x^2}+3\sqrt[3]{x}+1-x+3\sqrt[3]{x^2}-3\sqrt[3]{x}+1-6\sqrt[3]{x^2}+6\\ =8\)
Lời giải:
Gọi biểu thức là $A$
\(A=(x+3\sqrt[3]{x^2}+3\sqrt[3]{x}+1)-(x-3\sqrt[3]{x^2}+3\sqrt[3]{x}-1)-6(\sqrt[3]{x^2}-1)\)
\(6\sqrt[3]{x^2}+2-6(\sqrt[3]{x^2}-1)=8\) là giá trị không phụ thuộc vào biến.

\(A=s\left(x\right)cs\left(x\right)+\frac{\left(s^3\left(x\right)+cs^3\left(x\right)\right)}{cs\left(x\right)\left(1+t\left(x\right)\right)}=s\left(x\right)cs\left(x\right)+\left(\frac{\left(s\left(x\right)+cs\left(x\right)\right)\left(1-s\left(x\right)cs\left(x\right)\right)}{\left(s\left(x\right)+cs\left(x\right)\right)}\right)\)
\(=1\) vì \(s\left(x\right)+cs\left(x\right)\ne0,\forall0< =x< =\frac{\pi}{2}\)