Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AB và CD cắt nhau tại O là trung điểm mỗi đường nên ACBD là hình bình hành
=> AC//BD

x A y C t B x y
Câu a ta có :
At > yy (gt)
mà xx /yy (gt)
At yy ( hệ quả tiền đề Ô =lít)
câu b:
Vì AT tia phân giác xAb
=> xAt = =BaT =40 độ
Vậy :
bCE>BEC
~Study well~

a, Ta có: At∩xx′={A}(gt)At∩xx′={A}(gt)
Mà xx' // yy' (gt)
=> At ∩∩ yy' (hệ quả của tiên đề ơ-clit)
b,Tia At là phân giác góc xAB (gt)
=> góc xAt = góc BAt = Góc xAB / 2 = 80o/2 = 40o
Có: xx' // yy' (gt)
mà At ∩∩ yy' = {C} (gt)
=> Góc xAt = góc ACB = 40o (cặp góc so le trong )

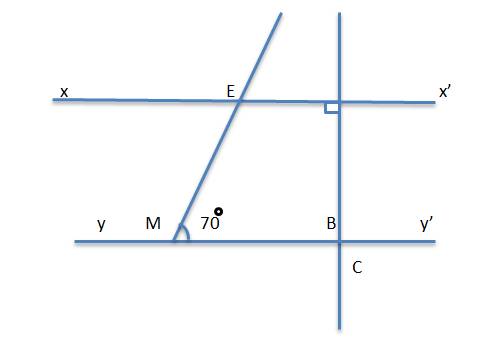
a) Ta có:
\(xx'\perp C\left(gt\right)\)
\(yy'\perp C\left(gt\right)\)
\(\Rightarrow xx'//yy'\)
b) Ta có: \(xx'//yy'\) và tia \(Mz\) cắt \(xx'\) nên:
\(\widehat{xEM}=\widehat{EMB}\) (so le trong)
\(\Rightarrow\widehat{xEM}=70^o\)
Mà: \(\widehat{xEM}\) đối đỉnh với \(\widehat{zEA}\) nên:
\(\Rightarrow\widehat{zEA}=\widehat{xEM}=70^o\)
\(\widehat{xEz}+\widehat{zEA}=180^o\) (kề bù)
\(\Rightarrow\widehat{xEz}=180^o-70^o=110^o\)
\(\widehat{MEA}+\widehat{xEM}=180^o\) (kề bù)
\(\Rightarrow\widehat{MEA}=180^o-70^o=110^o\)

Giải
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 180
0
(2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212180
0 = 90
0
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo
bởi hai đường thẳng cắt nhau đó.
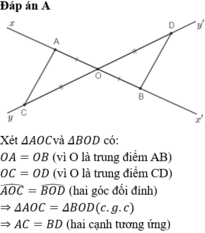
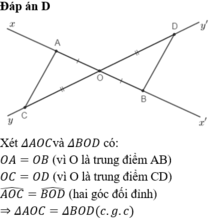
\(AC//BD\Rightarrow\widehat{CAM}=\widehat{DBM}\)
\(M\)trung điểm \(AB\Rightarrow AM=BM\)
\(\widehat{CMA}=\widehat{DMB}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta CAM=\Delta DBM\left(g.c.g\right)\Rightarrow AC=BD\)
Bạn Ngọc Khanh ơi đề bài chưa cho AC// BD ạ