Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
TKHT có f = 12 cm
Vật sáng AB cao 1cm đặt vuông góc với trục chính tại A.
Khoảng cách vật – tk: d= 8 cm.
a. Vẽ ảnh A’B’ của vật AB
b. Nêu đặc điểm của ảnh.
c. Tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh.
Giải:
a. Vẽ hình minh họa sự tạo ảnh
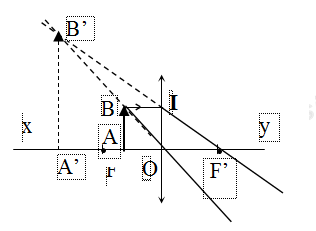
b. Vì vật nằm trong khoảng tiêu cự của thấu kính (d
c. Xét tam giác OAB và tam giác OA’B’ có: góc O chung; góc A = góc A’ = 900.
Nên tam giác OAB đồng dạng với tam giác OA’B’. Ta có các tỉ số đồng dạng:
ABA′B′=AOA′O⇔hh′=dd′ABA′B′=AOA′O⇔hh′=dd′
Xét tam giác OIF’ và tam giác F’A’B’
Có:
IF′O=ˆB′F′A′IF′O^=B′F′A′^
; ˆO=ˆA′=900O^=A′^=900
Nên tam giác OIF’ ~ tam giác F’A’B’ . Ta có tỉ số đồng dạng:
OIA′B′=OF′F′A′⇔ABA′B′=OF′OA′+OF′⇔dd′=fd′+fOIA′B′=OF′F′A′⇔ABA′B′=OF′OA′+OF′⇔dd′=fd′+f
Thay số từ đề bài ta có:
8d′=12d′+12⇔8d′+96=12d′⇔4d′=96⇔d′=24cm⇔hh′=dd′⇔h′=h.d′d=1.248=3cm

a. Bạn tự vẽ ( ảnh ảo )
b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\) ( do OI = AB ) (1)
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{8}{OA'}=\dfrac{12}{OA'+12}\)
\(\Leftrightarrow OA'=24\left(cm\right)\)
Thế \(OA'=24\) vào \(\left(1\right)\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{8}{24}\)
\(\Leftrightarrow A'B'=3\left(cm\right)\)
