Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A.\left(u+v\right)'=u'+v'\Rightarrow Sai\\ B.\left(uv\right)'=u'v+uv'\RightarrowĐúng\\ C.\left(\dfrac{1}{v}\right)'=-\dfrac{v'}{v^2}\Rightarrow Sai\\ D.\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}\Rightarrow Sai\)
\(\Rightarrow\) Chọn B

Đặt: \(g(x) = u(x).v(x),\,\,f(x) = g(x).w(x)\)
Ta có:
\(f'(x) = g'(x).w(x) + g(x).w'(x) = \left( {u.v} \right)'.w(x) + (uv).w'(x) = \left( {u'v + uv'} \right).w + (uv).w'\)\( = u'vw + uv'w + uvw'\)

A. Đúng (theo định nghĩa đạo hàm tại một điểm).
B. Đúng vì:
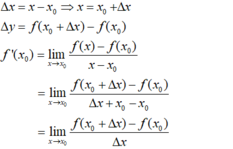
C. Đúng vì:
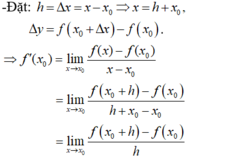
Chọn D

Đáp án D
- A. Đúng (theo định nghĩa đạo hàm tại một điểm).
- B. Đúng vì:
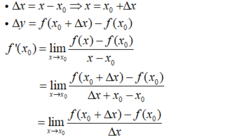
- C. Đúng vì:
+ Đặt:
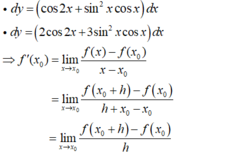

+ Nếu hàm số y= f(x) có đạo hàm tại điểm x0 thì hàm số sẽ liên tục tại điểm x0
+ Ngược lại, nếu hàm số liên tục tại điểm x0 thì chưa chắc hàm số đã có đạo hàm tại điểm x0.
+ Theo định nghĩa đạo hàm tại 1 điểm ta có:
f ' ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 và f ' ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x
Vậy D sai
Chọn D.

Thịnh ơi, có gì mấy câu trả lời SGK em giúp anh trình bày đầy đủ và làm đẹp nhé, có Latex đầy đủ á. Mình làm hướng đến cộng đồng, em giúp hoc24 nhé!
a) Ta có: \(\Delta x = x - {x_0},\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\)
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{h({x_0} + \Delta x) - h({x_0})}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{h\left( x \right) - h\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) + g(x) - f({x_0}) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g(x) - f\left( {{x_0}} \right)}}{{x - {x_0}}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{g\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( {{x_0} + \Delta x} \right) - g\left( {{x_0}} \right)}}{{\Delta x}}\end{array}\)
b) \(h'({x_0})\) = \(f'({x_0}) + g'({x_0})\)
Phát biểu D đúng.
Cái này theo công thức đạo hàm thôi
Chọn D