Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

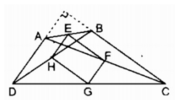
a, xét tam giác ABD có EA=EB <gt>, HB=HD <gt>=>EH//AD
Xét tam giác ADC có FC=FA<gt>, GD=GC<gt>=>FG//AD
=>EH//FG (1)
Chứng minh tương tự :Xét tam giác ABC =>EF//BC
Xét tam giác BDC =>HG//BC
=>EF//HG (2)
=> Tứ giác EFGH là hình bình hành
Kẻ AD vuông góc vs BC tại O
EH//AD, AD vuông góc vs AD => EH vuông góc vs BC
EF//BC , EH vuông góc vs BC =>EF vuông góc vs EH
=> Tứ giác EFGH có góc E=90 nên là hình chữ nhật
b, Chứng minh 2 cạn kề bằng nhau đi
c, Hình chữ nhật cũng là hình thoi
HÌnh thoi là hình vuông
=>hình thoi EFGH có góc E =90 <cmt> nên là hình vuông
Tẹt Sún tại sao tứ giác ABCD có cạnh AD mà lại kẻ Ad vuông góc với BC nữa vậy ?????

Xét ΔABC có
E,H lần lượt là trung điểm của AB,AC
=>EH là đường trung bình của ΔABC
=>EH//BC và EH=BC/2
Xét ΔBDC có
F,G lần lượt là trung điểm của DB,DC
=>FG là đường trung bình của ΔBDC
=>FG//BC và FG=BC/2
EH//BC
FG//BC
Do đó: EH//FG
EH=BC/2
FG=BC/2
Do đó: EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
Xét ΔBAD có
E,F lần lượt là trung điểm của BA,BD
=>EF là đường trung bình
=>EF//AD và EF=AD/2
Để EHGF là hình vuông thì EH=EF và EH\(\perp\)EF
EH=EF
EH=BC/2
EF=AD/2
Do đó: BC=AD
EH\(\perp\)EF
EH//BC
Do đó: EF\(\perp\)BC
EF\(\perp\)BC
EF//AD
Do đó: BC\(\perp\)AD
Vậy: Khi BC=AD và BC\(\perp\)AD thì EFGH là hình vuông

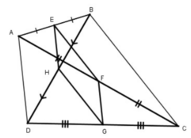
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình vuông khi và chỉ khi EFGH là hình chữ nhật đồng thời là hình thoi
⇔ AD ⊥ BC và AD = BC

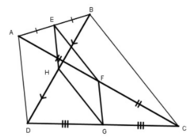
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC
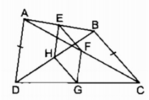

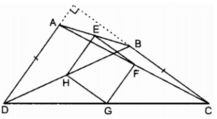
a: Xét ΔBAD có
E là tđiểm của AB
H là tđiểm của BD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//AD và EH=AD/2(1)
Xét ΔACD có
F là trung điểm của AC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔACD
Suy ra: FG//AD và FG=AD/2(2)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EFGH là hình bình hành

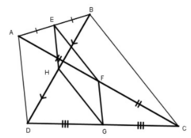
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC