Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối A vs N
a)xét tg CEF có: N là t/đ của EF(gt) và A là t/đ của FC (vì C đx vs F qua A) => AN là đg trung bình của tg CEF
=> AN//CE và AN =1/2. CE
=> AN=1/2.BC(vì BC = CE) => AN =BM(vì BM = 1/2. BC)
xét tg ANMB có: AN=MB (cmt) và AN//MB ( vì AN// CE ; B,M,C,E thẳng hàng) => tg ANMB là hbh=> MN//AB và AB=MN (1) ;
xét tg AGD có: I là t/đ của AG (gt) và K là t/đ của DG(gt) => IK là đg trung bình của tg AGD => IK=1/2.AD và IK //AD
Mà B là t/đ của AD (vì A đx vs D qua B) => AB=BD=1/2.AD=> IK=AB ( =1/2.AD) (2)
Từ (1),(2)=> IK=MN
Ta có: MN// AB(cmt) ; B thuộc AD => MN//AD
Xét tg MNIK có: IK=MN (cmt) và IK//MN (cùng // AD)
=> tg MNIK là hbh (đpcm)
b) Do tg MNIK là hbh ( câu a) mà G là gđ của IM và KN nên G là t/đ của IM là KN
=> IG=MG và KG=NG
Mặt khác: I là t/đ của AG(gt)=> IG=AI=> AI=IG=GM
K là t/đ của DG(gt) => Dk=KG => DK=KG=GN
xét tg ABC có: AM là đg trung tuyến (gt) và AI=IG=GM (cmt) => G là trọng tâm của tg ABC (*)
xét tg DEF có: DN là đg trung tuyến (gt) và DK=KG=GN(cmt) => G là trọng tâm của tg DEF (**)
Từ (*),(**) => G vừa là trọng tam của tg ABC vừa là trọng tâm của tg DEF
=> Tg ABC và tg DEF có cùng trọng tâm là G (đpcm)
Nối A vs N
a)xét tg CEF có: N là t/đ của EF(gt) và A là t/đ của FC (vì C đx vs F qua A) => AN là đg trung bình của tg CEF
=> AN//CE và AN =1/2. CE
=> AN=1/2.BC(vì BC = CE) => AN =BM(vì BM = 1/2. BC)
xét tg ANMB có: AN=MB (cmt) và AN//MB ( vì AN// CE ; B,M,C,E thẳng hàng) => tg ANMB là hbh=> MN//AB và AB=MN (1) ;
xét tg AGD có: I là t/đ của AG (gt) và K là t/đ của DG(gt) => IK là đg trung bình của tg AGD => IK=1/2.AD và IK //AD
Mà B là t/đ của AD (vì A đx vs D qua B) => AB=BD=1/2.AD=> IK=AB ( =1/2.AD) (2)
Từ (1),(2)=> IK=MN
Ta có: MN// AB(cmt) ; B thuộc AD => MN//AD
Xét tg MNIK có: IK=MN (cmt) và IK//MN (cùng // AD)
=> tg MNIK là hbh (đpcm)
b) Do tg MNIK là hbh ( câu a) mà G là gđ của IM và KN nên G là t/đ của IM là KN
=> IG=MG và KG=NG
Mặt khác: I là t/đ của AG(gt)=> IG=AI=> AI=IG=GM
K là t/đ của DG(gt) => Dk=KG => DK=KG=GN
xét tg ABC có: AM là đg trung tuyến (gt) và AI=IG=GM (cmt) => G là trọng tâm của tg ABC (*)
xét tg DEF có: DN là đg trung tuyến (gt) và DK=KG=GN(cmt) => G là trọng tâm của tg DEF (**)
Từ (*),(**) => G vừa là trọng tam của tg ABC vừa là trọng tâm của tg DEF
=> Tg ABC và tg DEF có cùng trọng tâm là G (đpcm)

Đáp án A
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
Phương trình đường tròn tâm D qua A; B là:
![]()
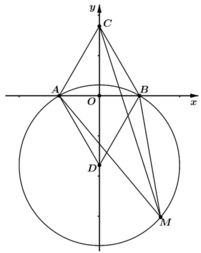
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
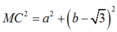

+ M nằm trên đường tròn (1) nên : 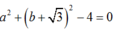
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.

*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D

a,vì N là trung điểm AC nên 2BN=BA+BC ta có
MA+NB+PC=1/2BA+1/2BC+NB=1/2 (BA+BC)+NB=1/2×2×BN+NB=BN+NB=0 (TM đề bài )
b, vì M;N;P làtrung điểm AB;AC;BC
2OM+2ON+2OP=OA+OB+OA+OC+OB+OC
=2OA+2OB+2OC
suy ra OM+ON+OP=OA+OB+OC
c,
Cm tương tự
2OB=OB'+OC
2OA=OA'+OB
2OC=OA+OC'
suy ra
2OA+2OB+2OC=OA+OB+OC+OA'+OB'+OC'
suy ra OA+OB+OC=OA'+OB'+OC'
Tứ giác DMCK có hai đường chéo cắt nhau tại trung điểm mỗi đường (N là trung điểm của MK và CD). Do đó, tứ giác DMCK là hình bình hành.
Theo quy tắc hình bình hành ta có:
Đáp án B