K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

19 tháng 10 2021
a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành

11 tháng 12 2021
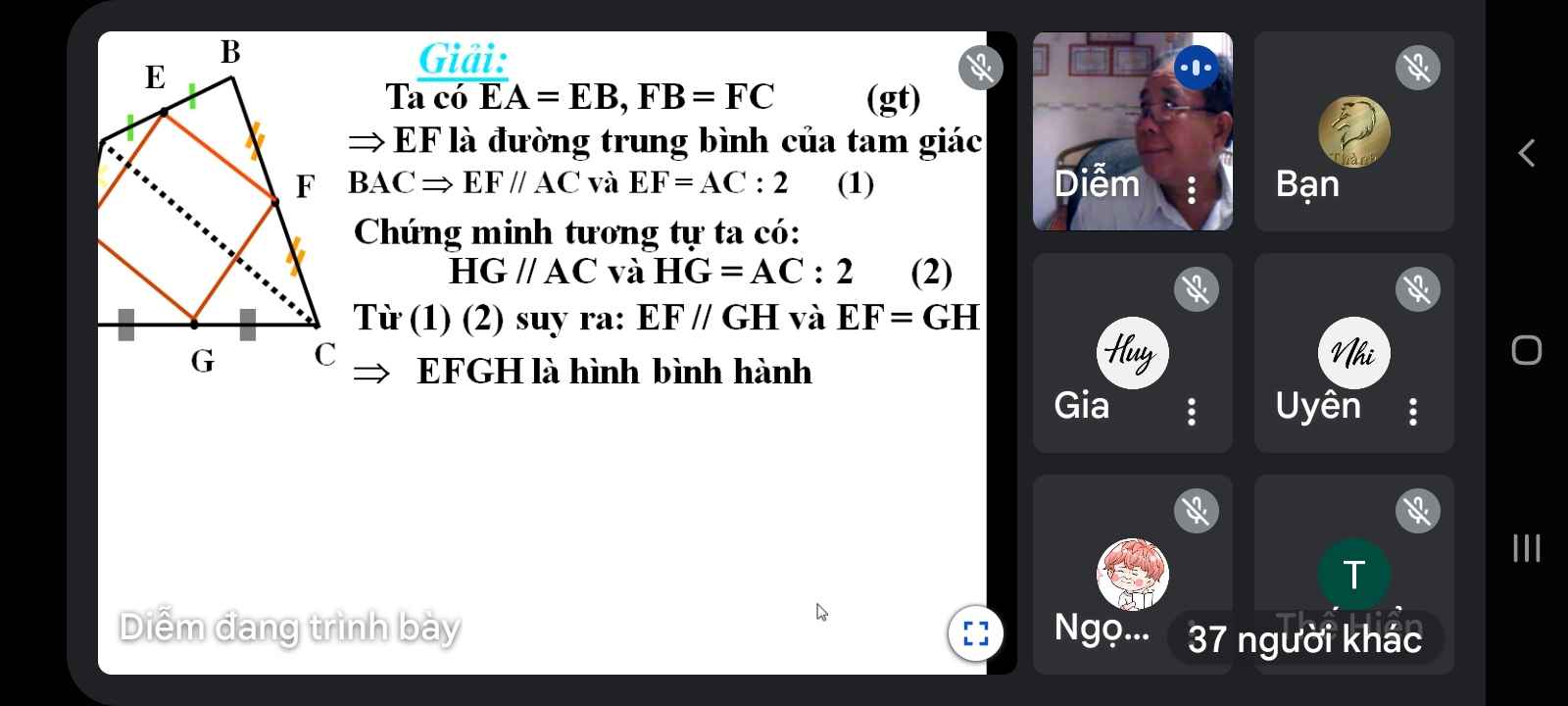
a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình của ΔABC
Suy ra: FE//AC và FE=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình của ΔCDA
Suy ra: GH//CA và GH=CA/2(2)
TỪ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hinh bình hành
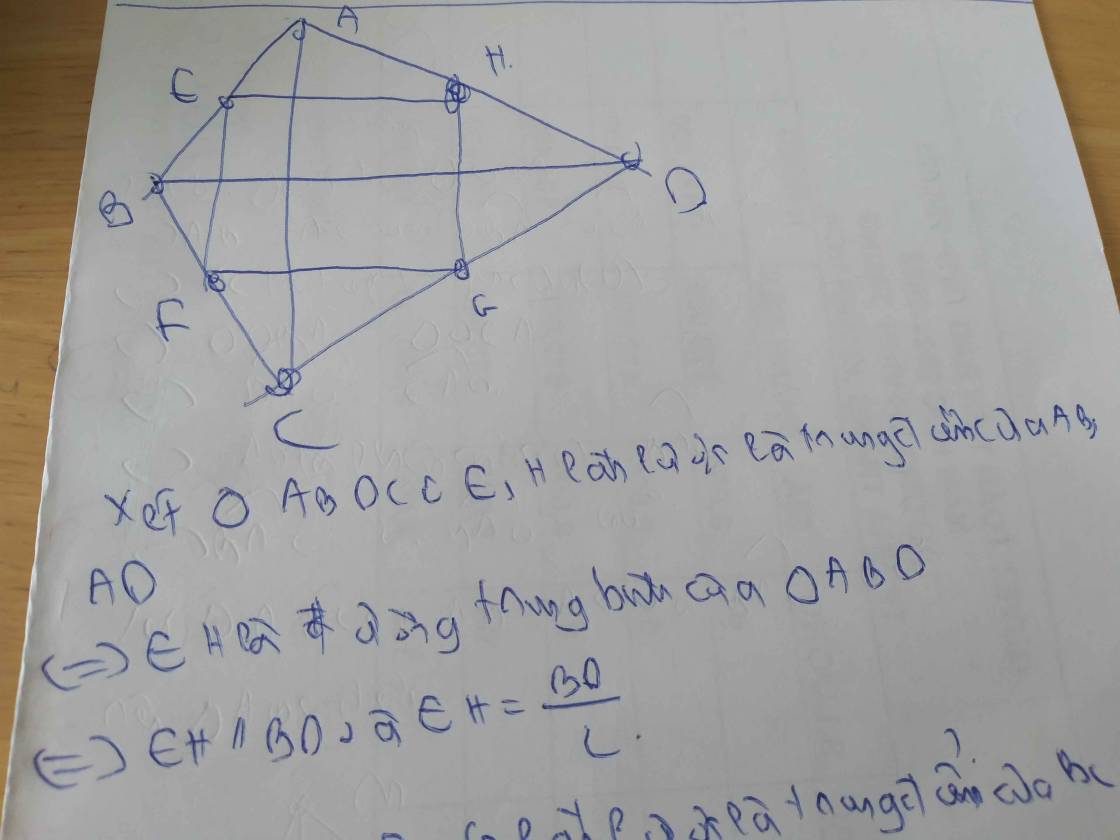



Xét ΔBAC có
E là trung điểm của BA(gt)
F là trung điểm của BC(gt)
Do đó: FE là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)
⇒FE//AC và \(FE=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔDAC có
H là trung điểm của AD(gt)
G là trung điểm của DC(gt)
Do đó: HG là đường trung bình của ΔDAC(Định nghĩa đường trung bình của tam giác)
⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra EF//HG và EF=HG
Xét tứ giác EFGH có
EF//HG(cmt)
EF=HG(cmt)
Do đó: EFGH là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Xét ΔBCD có
F là trung điểm của BC(gt)
G là trung điểm của CD(gt)
Do đó: FG là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)
⇒FG//BD và \(FG=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)(3)
Ta có: AC=BD(gt)
nên \(\dfrac{AC}{2}=\dfrac{BD}{2}\)(4)
Từ (2), (3) và (4) suy ra HG=FG
Hình bình hành EFGH có HG=FG(cmt)
nên EFGH là hình thoi(Dấu hiệu nhận biết hình thoi)
⇒\(S_{EFGH}=\dfrac{1}{2}\cdot EG\cdot HF=\dfrac{1}{2}\cdot5\cdot4=10cm^2\)