Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
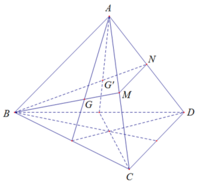
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

Đáp án D
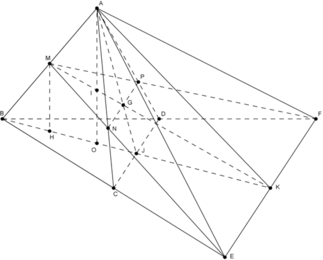
Vẽ AO ⊥ (BCD, MH ⊥ (BCD). Gọi K là trung điểm EF, ta có (ABK) ⊥ (BCD), mp (ABK) chứa AO, MH và là mặt phẳng trung trực của đoạn CD và EF.
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó MG = 1 3 MK (1) và AG = 2 3 AJ hay NP = 2 3 CD = 2 a 3 (vì NP//CD//EF và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là 3 2 a (và diện tích là 3 4 a 2 ).
Tam giác đều BCD cạnh a có đường cao BJ = 3 2 a , trọng tâm O, suy ra BO = 2 3 BJ = a 3 . Lại vì MH là đường trung bình trong tam giác vuông ABO nên
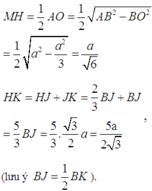
Vì tam giác MHK vuông tại H nên ta có
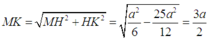
Quay lại (1), ta có
![]()
từ đó tính được diện tích tam giác MNP là
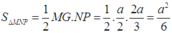

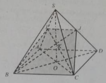
Gọi I là trung điểm CD thì G 1 ∈ B I , G 2 ∈ A I ⇒ mặt phẳng ( B G 1 G 2 ) chính là mặt phẳng (ABI) ⇒ Thiết diện là tam giác cân AIB.
Đáp án C
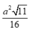
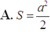


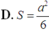
Trong (ABD), BN cắt AD tại F. Trong (ABC), BM cắt AC tại E.
Do M, N lần lượt là trọng tâm của ∆ABC và ∆ABD nên E, F lần lượt là trung điểm của AC, AD
Tứ diện ABCD có cạnh bằng a nên BE = BF = (a√3)/2
Thiết diện là tam giác cân BEF tại B, có đay EF = a/2
Diện tích BEF là
Đáp án D