Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

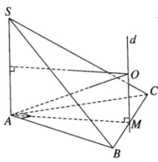
∠ BAC = 90 ° . Gọi M là trung điểm của BC, ta có MA = MB = MC. Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại M. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có OS = OA = OB = OC
![]()
Do đó ta có hình cầu tâm O ngoại tiếp tứ diện và có
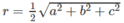

Đáp án D
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
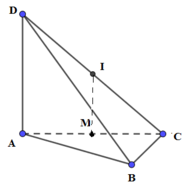
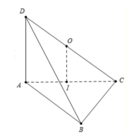
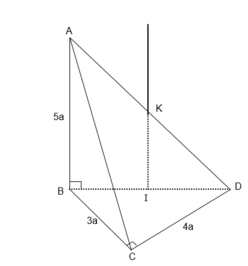
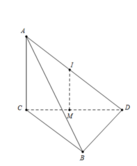
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:
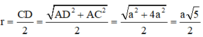

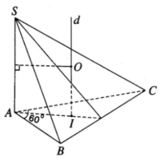
∠ BAC = 120 ° và b = c, khi đó ABC là một tam giác cân có góc A ở đỉnh bằng 120 ° và cạnh bên bằng b. Gọi M là trung điểm của cạnh BC. Kéo dài AM một đoạn MK = AM, ta có KA = KB = KC = AB = AC = b.
Dựng đường thẳng d vuông góc với mặt phẳng (ABC) tại K. Mặt phẳng trung trực của đoạn SA cắt d tại O.
Ta có: OS = OA = OB = OC và
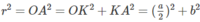
Do đó ta có mặt cầu tâm O ngoại tiếp tứ diện và có bán kính
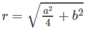
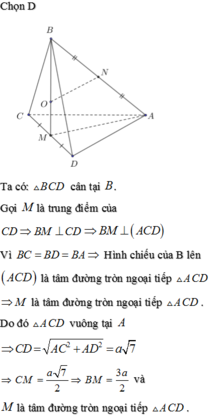


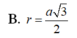
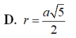
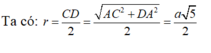
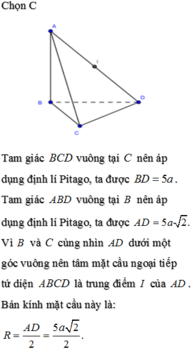
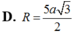

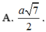
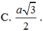
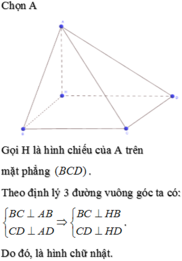

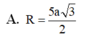
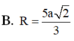
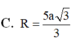


A D B C H a a
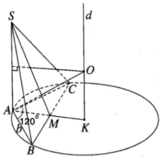
Gọi H là trung điểm BC
Vì \(\Delta BDC\) vuông tại D nên H là tâm đường tròn ngoại tiếp \(\Delta BDC\)
Vì \(\Delta ABC\) cân tại A nên AH vuông góc với BC
Mà (ABC) vuông góc (BDC) nên AH vuông góc với (BDC) tại H
\(\Rightarrow\) tâm mặt cầu ngoại tiếp tứ diện ABCD phải nằm trên đường thẳng AH
Chọn điểm O thuộc đường thẳng AH sao cho OA=OB thì O chính là tâm mặt cầu cần tìm
(bạn tự tính) được \(R=\frac{a^2}{b}\)