


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




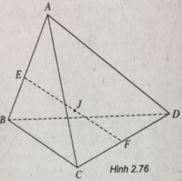
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
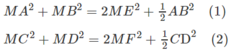
Cộng (1) và (2) ta có:
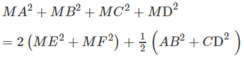
Gọi J là trung điểm của EF, ta có:
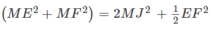
Khi đó:
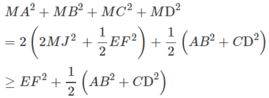
Vậy M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất khi M ≡ J.

A B C D H I (1;-2) ( 133 37 ; 58 37 ) BD:2x+y-4=0
1. \(\overrightarrow{AH}\left(\frac{96}{37};\frac{16}{37}\right)\). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => \(AB:6\left(x-1\right)+\left(y+2\right)=0\Leftrightarrow6x+y-4=0\)
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> \(CD:6\left(x-\frac{133}{37}\right)+\left(y+\frac{58}{37}\right)=0\Leftrightarrow6x+y-20=0\)
2. Xét hệ \(\hept{\begin{cases}2x+y=4\\6x+y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=4\end{cases}\Rightarrow}B\left(0;4\right)}\)
\(\hept{\begin{cases}2x+y=4\\6x+y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-4\end{cases}\Rightarrow}D\left(4;-4\right)}\)
BD và AC có trung điểm là \(I\left(2;0\right)\), suy ra \(C\left(3;2\right)\).
3. Ta có: \(MA^2+MC^2=2MI^2+\frac{AC^2}{2};MB^2+MD^2=2MI^2+\frac{BD^2}{2}\)
\(\Rightarrow MA^2+MB^2+MC^2+MD^2=4MI^2+\frac{AC^2+BD^2}{2}\ge\frac{AC^2+BD^2}{2}\)(không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
1. →AH(9637 ;1637 ). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => AB:6(x−1)+(y+2)=0⇔6x+y−4=0
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> CD:6(x−13337 )+(y+5837 )=0⇔6x+y−20=0
2. Xét hệ {
| 2x+y=4 |
| 6x+y=4 |
⇔{
| x=0 |
| y=4 |
⇒B(0;4)
{
| 2x+y=4 |
| 6x+y=20 |
⇔{
| x=4 |
| y=−4 |
⇒D(4;−4)
BD và AC có trung điểm là I(2;0), suy ra C(3;2).
3. Ta có: MA2+MC2=2MI2+AC22 ;MB2+MD2=2MI2+BD22
⇒MA2+MB2+MC2+MD2=4MI2+AC2+BD22 ≥AC2+BD22 (không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).

- Gọi A’ là điểm đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : \(\left|MA-MB\right|=\left|MA'-MB\right|=A'B\)
. Giả sử tồn tại một điểm M’ khác với M trên d , khi đó : \(\left|M'A-M'B\right|=\left|M'A'-M'B\right|\le A'B\)
Dấu bằng chỉ xảy ra khi M’A’B thẳng hàng, nghĩa là M trùng với M’.

Gọi D là trung điểm BC và G là trọng tâm tam giác ABC
Theo tính chất trọng tâm: \(AG=\dfrac{2}{3}AD\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=\left|\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{BA}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=\left|-2\overrightarrow{AD}\right|\)
\(\Leftrightarrow MG=\dfrac{2}{3}AD=AG\)
\(\Rightarrow\) Tập hợp M là mặt cầu tâm G bán kính AG với G là trọng tâm tam giác ABC