Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong (BCD): DG \cap∩ BC = F
Vậy DG \cap∩ (ABC) = F.
b. Cách 1: MG \subset⊂ (BMG) \equiv≡ (ABH) (H = BG \cap∩ DC)
(Do mặt phẳng (BMG) "lơ lửng" trong hình chóp nên ta kéo dài BM thành BA và BG thành BH để ta có cái nhìn dễ dàng hơn đối với mặt phẳng này).
(BMG) \cap∩ (ACD) =AH
Trong (ABH): MG \cap∩ AH =K
Vậy MG \cap∩ (ACD) = K.
a. Trong (BCD) có GD và BC cắt nhau tại K
vậy K = GD và (ABC)
b. có MG ⊂ (BMG) trùng (ABH) có H = BG và DC
(BMG) và (ACD) = AH
Trong (ABH) có MG và AH = P
Vậy MG và (ACD) = P

Ko chắc sẽ đúng
a)* Trên mp ABCD kéo dài MN và AB sao cho MN cắt AB = { I }
Xét mp (SMN) và (SAB) có:
S là điểm chung (1)
I là điểm chung (2)
=> (SMN) n (SAB) = { SI }
* Vì I thuộc mp ABCD (cmt)
G là trọng tâm tam giác SAB
Xét mp (GMN) và (SAB) có:
G và I là điểm chung
=> (GMN) n (SAB) = {GI}

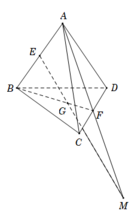
Vì G là trọng tâm tam giác BCD và F là trung điểm của CD nên G thuộc (ABF)
Ta có E là trung điểm của AB nên E thuộc ( ABF).
Gọi M là giao điểm của EG và AF mà A F ⊂ A C D suy ra M thuộc (ACD).
Vậy giao điểm của EG và mp (ACD) là giao điểm M của EG và AF
Chọn B.
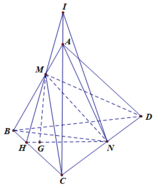


Trong mặt phẳng (ABD) nối MN cắt AD kéo dài tại P
Trong mặt phẳng (ACD) nối PG kéo dài cắt AC tại Q
MQ chính là giao tuyến của (GMN) và (ABC)