Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(Vẽ hình: A là đỉnh của tứ diện, BCD là đáy của tứ diện)
+ Trên mặt phẳng đáy BCD kẻ các đường cao của tam giác BCD là BE, CF, DK.Ba đường cao gặp nhau tại H.
+ Xét mặt phẳng ABE
CD vuông góc BE
CD vuông góc AB
=> CD vuông góc với mặt phẳng ABE => CD vuông góc với AH (1)
+ Xét mặt phẳng ACF
BD vuông góc AC
BD vuông góc CF
=> BD vuông góc với mặt phẳng ACF => BD vuông góc với AH (2)
+ Từ (1) và (2) => AH vuông góc BCD
=> AH vuông góc với BC
Mà BC vuông góc với DK
=> BC vuông góc với mp ADK => BC vuông góc với AD
Cho tứ diện ABCD. Chứng minh rằng:
\(\left(AB+CD\right)^2+\left(AD+BC\right)^2>\left(AC+BD\right)^2\)
Từ \(2\overrightarrow{ỊJ}=\overrightarrow{AB}+\overrightarrow{CD}\) suy ra
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2+4IJ^2\Leftrightarrow CB^2+DA^2=CA^2+DB^2+2AB^2.CD^2\)
\(\Leftrightarrow2.\overrightarrow{AB}\overrightarrow{CD}=AD^2-AC^2+BC^2-BD^2\)
Giả sử AB ⊥ CD ta phải chứng minh:
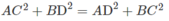
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
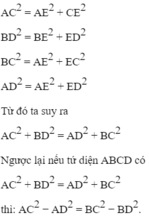
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho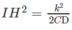 
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .
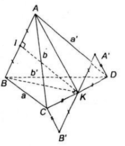
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
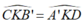( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
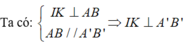
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD
