K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
5 tháng 8 2018
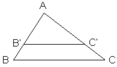
Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
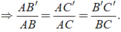
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )
CC
0

VT
0


24 tháng 2 2022
Bài 2:
a: AE=AC-CE=16-13=3(cm)
AD=AB-BD=8-2=6(cm)
Xét ΔAED và ΔABC có
AE/AB=AD/AC
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔABC
b: Ta có: ΔAED∼ΔABC
nên AE/AB=AD/AC
hay AB/AC=AE/AD
Xét ΔABE và ΔACD có
AB/AC=AE/AD
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD
Suy ra: \(\widehat{ABE}=\widehat{ACD}\)

Áp dụng bất đẳng thức tam giác, trong tam giác ABC có:
BC - AC < AB < BC + AC
=> 8 - 2 < AB < 8 +2
=> 6 < AB < 10
Mà độ dài của AB là số nguyên tố => AB = 7 cm
Vậy AB = 7 cm