Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta co: AB2+AC2=100 Ma BC2=100
\(\Rightarrow\Delta ABC\)vuong tai A
A, Trong \(\Delta ABC\)co AD la phan giac
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tinh chat duong phan giac)
\(\Rightarrow\frac{AB}{AB+AC}=\frac{BD}{BD+DC}\)\(\Rightarrow\frac{8}{8+6}=\frac{BD}{10}\Rightarrow BD=\frac{8.10}{14}=\frac{40}{7}cm\)
ta co: BD+DC=BC\(\Rightarrow DC=BC-BD=10-\frac{40}{7}=\frac{30}{7}cm\)
B, Ke duong cao AH
ta co: \(S_{\Delta ABD}=\frac{1}{2}AH.BD\)va \(S_{\Delta ACD}=\frac{1}{2}AH.DC\)
\(\Rightarrow\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}=\frac{40}{7}:\frac{30}{7}=\frac{4}{3}\)

Gọi H là chân đường cao kẻ từ A -> BC
Áp dụng t/c đg p/g vào tg ABC ta có:\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{15}{20}=\frac{3}{4}\)
Mà \(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{CD}=\frac{3}{4}\) (theo trên)
Vậy tỉ số diện tích tg ABD và tg ACD là 3/4
Gọi H là chân đường cao kẻ từ A đến BC
Theo tính chất đường phân giác trong taam giác ABC, ta có:
\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{15}{20}=\frac{3}{4}\)
Ta có: \(\frac{S_{\Delta ABD}}{S_{\Delta ADC}}=\frac{\frac{1}{2}AH.DB}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{3}{4}\)
A C D B 15cm 20cm 25cm

A B C 6 8 H
a, Xét tam giác ABC và tam giác HBA ta có :
^ABC = ^HBA
^BAC = ^BHA = 900
Vậy tam giác ABC ~ tam giác HBA ( g.g )
b, Xét tam giác HAB và tam giác HCA ta có :
^AHB = ^CHA = 900
^BAH = ^HCA ( phụ nhau )
Vậy tam giác HAB ~ tam giác HCA ( g.g )
\(\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH.CH\)
c, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64\Rightarrow BC=10\)cm
Vì tam giác ABC ~ tam giác HBA ( cma )
\(\Rightarrow\frac{AC}{AH}=\frac{BC}{AB}\)( tỉ lệ thức )
\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=\frac{48}{10}=\frac{24}{5}\)cm

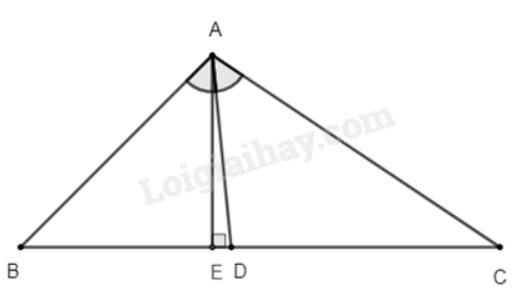
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).

a) Xét tam giác BAD và CAD có:
AB=AC=14cm
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác)
AD cạnh chung
=> \(\Delta BAD=\Delta CAD\left(c.g.c\right)\)
=> BD=CD
Mà BD+CD=BC=12 cm
=> BD=DC=12:2=6(cm)
b) Vì AB=AC, BD=DC
=> AD là đường trung trực của BC
=> AD _|_ BC
=> \(S_{\Delta ABD}=\frac{1}{2}AD\cdot BD;S_{\Delta CAD}=\frac{1}{2}AD\cdot DC\)
\(\frac{S_{\Delta ABD}}{S_{\Delta CAD}}=\frac{AD\cdot BD}{AD\cdot DC}=\frac{AD}{DC}=1\)
a) tg ABC có AD là tia phân giác =>CD/AC=BD/AB=CD+BD/AC+AB=5/7.
CD/AB=5/7=>CD=5/7*AB=40/7(cm)
Tương tự ta cx tính dc DC=30/7(cm).
b) Kẻ AH vuông góc với BC. ta có:
SABD=1/2*AH*BD. SACD=1/2*AH*CD.=>SABD/SACD=BD/CD=3/4