Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Do mình đánh máy hơi nhanh nên bị lỗi mấy phần cuối. Sorry cậu.
Câu d bị lỗi nên mình xin phép chỉnh sửa ở đây nhé!
d) \(\widehat{ABG}\) = \(\widehat{ACG}\)
- Ta có: AH là đường trung trực của BC
mà G ∈ AH (CM câu c)
⇒ GB = GC (tính chất đường trung trực)
⇒ Δ GBC cân tại G
- Ta có: Δ ABC cân tại A (giả thiết)
⇒ \(\widehat{ABC}\) = \(\widehat{ACB}\)
mà \(\widehat{GBC}\) = \(\widehat{GCB}\) (vì Δ GBC cân tại G, CMT)
⇒ \(\widehat{ABC}-\widehat{GBC}=\widehat{ACB}-\widehat{GCB}\)
⇒ \(\widehat{ABG}=\widehat{ACB}\left(đpcm\right)\)

b, Cho BH = 8cm, AH = 10cm. Tính AH này là sao , biết AH mà còn bắt tính AH

Bai 1:
Ap dung dinh li Py-ta-go vao tam giac AHB ta co:
AH^2+BH^2=AB^2
=>12^2+BH^2=13^2
=>HB=13^2-12^2=25
Tuong tu voi tam giac AHC
=>AC=20
=>BC=25+16=41

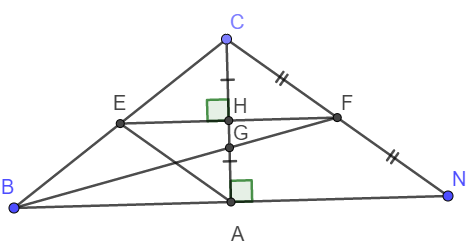
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 \(\Rightarrow ab=20\left(cm\right)\)
Xét tam giác ABC có:
AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
\(\Rightarrow\Delta EHC=\Delta EHA\) (Hai cạnh góc vuông)
Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)
\(\Rightarrow\widehat{EBA}=\widehat{EAB}\) (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CE=CF'\)
Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
Bài giải :

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 ⇒ab=20(cm)
Xét tam giác ABC có:
AC < AB < BC nên ^CBA<^BCA<^BAC.
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
⇒ΔEHC=ΔEHA (Hai cạnh góc vuông)
Do ΔEHC=ΔEHA⇒^ECA=^EAC
⇒^EBA=^EAB (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
AGAC =13 ⇒AG=15 .15=5(cm)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH (Cạnh góc vuông và góc nhọn kề)
⇒CE=CF'
Lại có CE=12 BC=12 CN⇒CF'=12 CN
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.

HÌNH TỰ VẼ NHA![]()
a. Vì △ ABC cân tại A => AB=AC
góc ABC=ACB
Xét △ABH và △ACH có:
AB=AC
góc ABH=ACH
góc BAH=CAH ( tia phân giác AH của góc BAC )
=> △ABH =△ACH ( g.c.g )
b, Có △ABH =△ACH => BH=HC
=> AH là đường trung tuyến △ ABC
Có: BD cũng là trung tuyến △ ABC
mà AH và BD cắt nhau tại G
=> G là trọng tâm của △ABC
△ABH =△ACH => góc AHB=AHC = 90 độ
Xét tam giác AHB vuông tại H , ta có:
\(AB^2=AH^2+BH^2\)
=> \(15^2=AH^2+9^2\)
=> \(AH^2=144\)
=> AH=12
Có G là trọng tâm => \(\dfrac{AG}{AH}=\dfrac{2}{3}\)
=> AG =\(12.\dfrac{2}{3}=8\)
Câu (c) có vẻ như đề bài sai.

a) Xét tam giác HAB và HAC ,ta có :
Cạnh AH chung (1)
\(\widehat{BAH}=\widehat{CAH}\)( phân giác AH ) (2)
AB = AC ( gt )(3)
Từ (1)(2)(3) => tam giác HAB = HAC ( c. g. c )
b) Ta có trong tam giác cân ABC có AH là đường cao cũng là đường trung tuyến
=> G là giao của2 đường trung tuyến AH và BD
=> G là trọng tâm của tam giác ABC
p/s tham khảo

a ) Xét ∆BAD và ∆CAD
AB = AC ( ∆ABC cân )
\(\widehat{B}=\widehat{C}\)
\(\widehat{BAD}=\widehat{DAC}\)
=> ∆ABH = ∆ACH(g.c.g)
Ta có hình vẽ:
A B C H G
a/ Ta có: tam giác ABC cân
Mà AH là đường cao của tam giác ABC
nên AH cũng là đường trung tuyến
=> BH = HC = 1/2 BC = 1/2 . 6 = 3 cm
Ta có: tam giác ABH vuông tại H
=> AB2 = AH2 + BH2
=> 52 = AH2 + 32
=> AH2 = 25 - 9 = 16
=> AH = 4 cm
Vậy BH = 3cm; AH = 4 cm.
b/ Ta có: AH là trung tuyến của tam giác ABC
Mà G là trọng tâm của tam giác
=> G \(\in\) AH
Vậy A;G;H thẳng hàng. (đpcm).
ΔABC cân tại A
có đường cao AH (gt)
\(\Rightarrow AH\) là đường trung tuyến ΔABC
\(\Rightarrow\) BH = CH = \(\dfrac{BC}{2}=3\)
ΔvgHAB có \(AB^2=AH^2+BH^2\)
\(\Rightarrow\) \(AH^2=AB^2-BH^2\)
\(\Rightarrow\) \(AH^2=5^2-3^2=16\)
\(\Rightarrow\) \(AH=4\)
b) Do G là trọng tâm ΔABC ( gt)
\(\Rightarrow\)AG là đường trung tuyến của ΔABC
⇒ AG đi qua trung điểm của BC (1)
mà H là trung điểm của BC (gt) (2)
(1)(2) \(\Rightarrow\) A ; G ; H thẳng hàng
c) Mình nghĩ là chứng minh \(\widehat{ABG}=\widehat{ACG}\) thì đúng hơn nên mình sửa lại nha /=/
ΔABC cân tại A
có đường cao AH (gt)
\(\Rightarrow AH\) là đường phân giác \(\widehat{BAC}\)
\(\Rightarrow\)\(\widehat{BAG}=\widehat{CAG}\)
Xét ΔABG và ΔACG
có AG cạnh chung
\(\widehat{BAG}=\widehat{CAG}\) (cmt)
AB = AC (gt)
\(\Rightarrow\)ΔABG = ΔACG ( c_g_c)
\(\Rightarrow\) \(\widehat{ABG}=\widehat{ACG}\)