Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số có 4 chữ số có dạng ![]()
Số phần tử của không gian mẫu: n(S)=9.9.8.7=4536.
Gọi A: “ tập hợp các số tự nhiên có 4 chữ số phân biệt và lớn hơn 2500.”
TH1: a>2
Chọn a: có 7 cách chọn.
Chọn b: có 9 cách chọn.
Chọn c: có 8 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có:7.9.8.7=3528 .
TH2: a=3; b>5
Chọn a: có 1 cách chọn.
Chọn b: có 4 cách chọn.
Chọn c: có 8cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.4.8.7=224 (số).
TH3: a=2; b=5; c>0
Chọn a: có 1 cách chọn.
Chọn b: có1 cách chọn.
Chọn c: có 7 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.7.7=49(số).
TH4. a=2; b=5; c=0 ;d>0
Chọn a: có 1 cách chọn.
Chọn b: có 1 cách chọn.
Chọn c: có 1 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.1.7=7(số).
Như vậy: n(A)=3528+224+49+7=3808
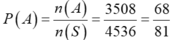
Chọn C.

Xét số ![]() được lập từ các chữ số thuộc tập A.
được lập từ các chữ số thuộc tập A.
Vì x lẻ nên e ∈ {1; 3; 5; 7} , suy ra có 4 cách chọn e. Bốn chữ số còn lại được chọn từ 7 chữ số của tập A \ {e} nên có cách
Suy ra, có 4.840=3360 số lẻ gồm năm chữ số khác nhau.
Mà số x bắt đầu bằng 123 có số.
Vậy số x thỏa yêu cầu bài toán là :3360- 20=3340 số.
Chọn A.

Xét tập B={ 1;4;5;6;7;8}, ta có B không chứa số 3.
X là một tập con của A thỏa yêu cầu bài toán khi và chỉ khi X \ {2} là một tập con của B . Do đo, số tập con của A thỏa yêu cầu bài toán bằng số tập con của B và bằng 26 = 64
Chọn A.

Chọn D.
Ta có 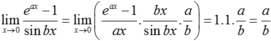
Vậy để 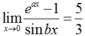 thì
thì 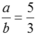 . Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
. Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
+ 15k2 = 15 ⇔ k2 = 1 ⇒ k = 1 ⇒ ab = 15.
+ 15k2 = 60 ⇔ k2 = 4 ⇒ k = 2 ⇒ ab = 60.
+ 15k2 = 240 ⇔ k2 = 16 ⇒ k = 4 ⇒ ab = 240.
Vậy cả ba đáp án đều đúng.

a.
\(u_5=18\Rightarrow u_1+4d=18\) (1)
\(4S_n=S_{2n}\Rightarrow\dfrac{4n\left(2u_1+\left(n-1\right)d\right)}{2}=\dfrac{2n\left(2u_1+\left(2n-1\right)d\right)}{2}\)
\(\Rightarrow4u_1+2\left(n-1\right)d=2u_1+\left(2n-1\right)d\)
\(\Rightarrow2u_1-d=0\Rightarrow d=2u_1\) (2)
Thế (2) vào (1):
\(\Rightarrow9u_1=18\Rightarrow u_1=2\Rightarrow d=4\)
b.
Do a;b;c là 3 số hạng liên tiếp của 1 CSC công sai 2 nên: \(\left\{{}\begin{matrix}b=a+2\\c=a+4\end{matrix}\right.\)
Khi tăng số thứ nhất thêm 1, số thứ 2 thêm 1 và số thứ 3 thêm 3 được 1 cấp số nhân nên:
\(\left(a+1\right)\left(c+3\right)=\left(b+1\right)^2\)
\(\Rightarrow\left(a+1\right)\left(a+7\right)=\left(a+3\right)^2\)
\(\Rightarrow a^2+8a+7=a^2+6a+9\)
\(\Rightarrow a=1\Rightarrow b=3\Rightarrow c=5\)

- Gọi d là tiếp tuyến của đồ thị hàm số đã cho qua A( 0, 2)
→ phương trình của d có dạng: y = k(x - 0) + 2 hay y = kx + 2
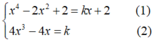
- Thay (2) vào (1) ta được :
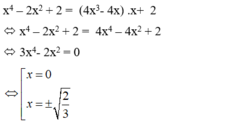
- Tương ứng với ba giá trị của x ta vừa tìm được, ta viết được 3 tiếp tuyến đi qua Ađến đồ thị (C).
Chọn B.
có 18 số cần tìm.
gọi số cần tìm là abc
xét a=1, c có 3 cách chọn(0,2,8), b có 4 cách => có 3*4=12
xét abc<270, a=2, nếu c=8 thì b có 3 cách, nếu c=0 thì b có 2 cách => có 1*1*3+1*1*2=6
xét 270 đến 278, ko có số thảo mãn