Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
\(\sin65^0=\cos25^0\)
\(\cos70^0=\sin20^0\)
\(\tan80^0=\cot10^0\)
\(\cot68^0=\tan22^0\)

Bài 1:
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=1.8^2+2.4^2=3^2\)
hay BC=3cm
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2.4}{3}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1.8}{3}=\dfrac{3}{5}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2.4}{1.8}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{1.8}{2.4}=\dfrac{3}{4}\)

a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)

a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)

sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
a) b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC
b) b = c. (b/c) = c.tgB = c.cotgC
c = b.(c/b) = b.cotgB = b.tgC

\(BC^2=AB^2+AC^2=36+64=100=10^2\)
\(\Rightarrow BC=10\left(cm\right)\)
\(SinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow SinC=Sin\left(90-B\right)=CosB=\dfrac{3}{5}\)
\(CosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow CosC=Cos\left(90-B\right)=SinB=\dfrac{4}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow tanC=tan\left(90-B\right)=CotB=\dfrac{3}{4}\)
\(CotB=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow cotC=cot\left(90-B\right)=tanB=\dfrac{4}{3}\)

Đổi AB=60mm=6cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
\(\left\{{}\begin{matrix}\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\\\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\\\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\end{matrix}\right.\)
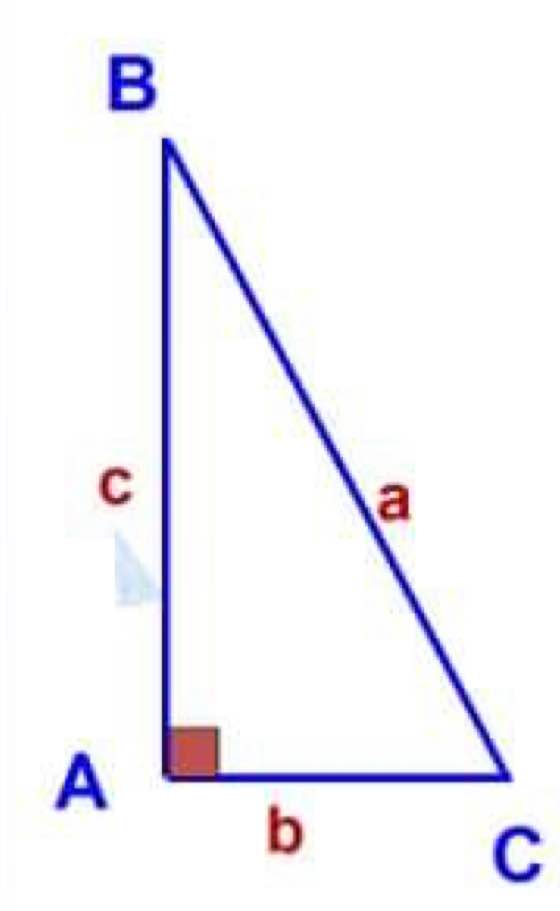
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}\)
\(cosB=\dfrac{AB}{BC}\)
\(tanB=\dfrac{AC}{AB}\)
\(cotB=\dfrac{AB}{AC}\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
\(cosC=\dfrac{AC}{BC}\)
\(tanC=\dfrac{AB}{AC}\)
\(cotC=\dfrac{AC}{AB}\)
Nhận xét:
\(sinB=cosC\)
\(sinC=cosB\)
\(tanB=cotC\)
\(cotB=tanC\)