Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
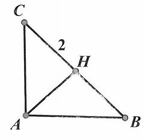
Khối tròn xoay tạo thành 2 khối nón, đó là: khối nón đỉnh B, đường sinh AB và khối nón đỉnh C đường sinh CA. Thể tích khối tròn xoay được tạo thành là: V = 2. 1 3 π .1 2 .1 = 2 π 3 .

Chọn D
Tam giác ABC quay quanh trục là đường thẳng BC tạo ra hai khối nón:
-Khối nón đỉnh B, đường sinh BA.
-Khối nón đỉnh C, đường sinh CA.
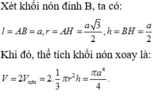

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
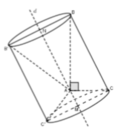
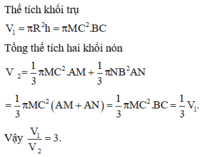

Đáp án D.
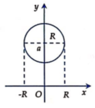
Ta có
x 2 + y − a 2 = R 2 ⇔ y = a ± R 2 − x 2
Nửa trên hình tròn có phương trình là y = a + R 2 − x 2
Nửa dưới hình tròn có phương trình là y = a − R 2 − x 2
Thể tích của hình xuyến là
V = V 1 − V 2 = π ∫ − R R a + R 2 − x 2 2 d x − π ∫ − R R a − R 2 − x 2 2 d x = 4 π a ∫ − R R R 2 − x 2 d x
Đặt x = R sin t ⇒ d x = R costdt x = − R ⇒ t = − π 2 ; x = R = t = π 2
⇒ V = 4 π a ∫ − π 2 π 2 R 2 − R 2 sin 2 t . R cos t d t = 4 π a R 2 ∫ − π 2 π 2 cos 2 t d t = 2 π 2 a R 2

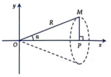
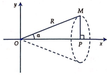
a) Hoành độ điểm P là :
xp = OP = OM. cos α = R.cosα
Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:
b) Đặt t = cosα => t ∈ . (vì α ∈
), α = arccos t.
Ta có :
V' = 0 ⇔
hoặc (loại).
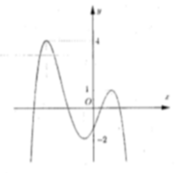
Ta có bảng biến thiên:
Từ đó suy ra V(t) lớn nhất ⇔ , khi đó :
.




Đáp án A.
Tam giác OPM vuông tại P suy ra O P = R . cos α ; M P = R . sin α .
Thể tích khối nón được tính bằng công thức
V = 1 3 . O P . πMP 2 = 1 3 . R . cosα . π . R 2 . sin 2 α = πR 3 3 . cosα . sin 2 α = πR 3 3 . cosα 1 - cos 2 α
V đạt giá trị lớn nhất khi - cos 3 α + cos α đạt giá trị lớn nhất.
Sử dụng TABLE ta có
Ta thấy hàm số đạt giá trị lớn nhất là 0 , 384 = 2 3 9 . Suy ra V = 2 3 πR 3 27 .